Este post dedicado a amostra por conglomerados encerra o primeiro bloco de publicações dedicadas a amostragem probabilística.
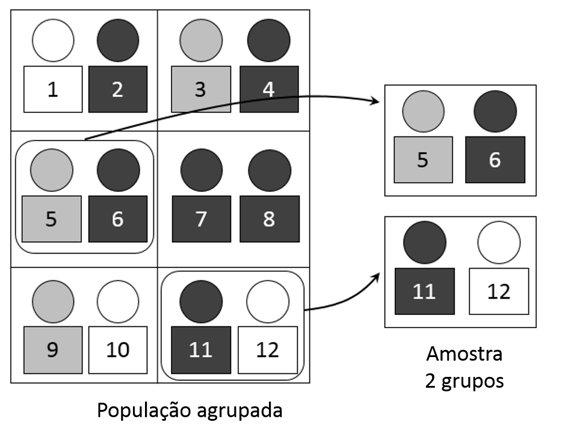
A amostra por conglomerados é uma técnica que explora existência de grupos (clusters) na população. Esses grupos representam adequadamente a população total em relação a característica que queremos medir. Em outras palavras, estes grupos contêm variabilidade da população inteira. Se isso acontecer, você pode selecionar apenas alguns desses conglomerados para realizar o estudo, conforme ilustra a figura.
Podemos ver esta técnica a partir de outro ponto de vista. Enquanto todas as técnicas de amostragem estudadas até agora as unidades da amostra coincidem com os indivíduos a serem estudados, na amostra por conglomerados, a unidades de amostra são grupos do estudo, o que pode ser muito benéfico em relação ao custo de amostragem em si. Em troca, é comum obter uma menor precisão ao utilizar esta técnica, causada pela falta de heterogeneidade dentro dos conglomerados.
O processo da amostra
O primeiro passo para aplicar essa técnica consiste em definir os aglomerados. Trata-se de identificar uma característica que permita dividir a população em grupos distintos (não sobrepostos) e exaustivos (todos os indivíduos devem estar em um grupo), de modo que os grupos não diferem em relação ao que queremos medir. Uma vez que tenhamos definido esses agrupamentos, basta selecionar aleatoriamente alguns deles para estudo.
Um critério bastante habitual para definir os conglomerados são os clusters geográficos. Por exemplo, se queremos estudar qual a proporção de argentinos que fumam, podemos dividir o total da população em províncias e selecionar algumas delas para estudo. Se não temos um parâmetro para a % de fumantes, que poderia variar de uma província a outra, esta solução vai permitir uma concentração de amostragem em uma única área geográfica. Se o estudo for realizado através de entrevistas pessoais, esta técnica representaria uma economia significativa nos custos de viagem.
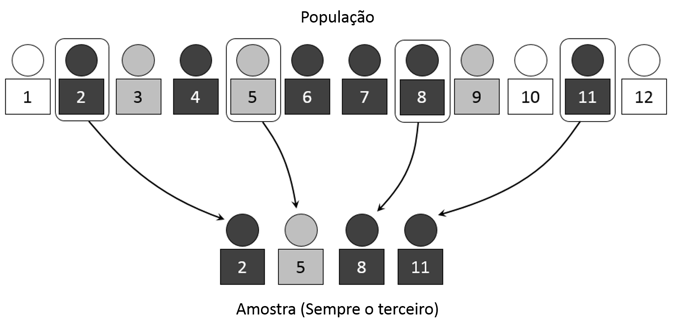
Uma vez definido os conglomerados, o próximo passo é selecionar os grupos para realizar o estudo, por amostragem aleatória simples ou amostragem sistemática.
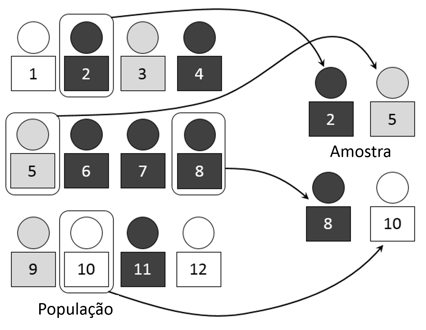
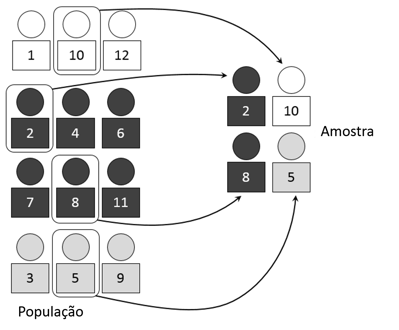
Por último, uma vez que selecionados os conglomerados, podemos pesquisar a todos os indivíduos que formam parte dos mesmos grupos, ou aplicar uma outra técnica de amostragem dentro do cluster, como por exemplo, realizar uma amostragem aleatória simples ou sistemática. Se optarmos por essa possibilidade, estamos falando de uma amostra de duas etapas ou bietápica: a primeira etapa é a seleção do conglomerado e a segunda é a dos indivíduos dentro do cluster. Se em vez disso, estudarmos todos os indivíduos conglomerados, estaremos realizando uma amostragem por conglomerados unietápica.
Amostra estratificada e amostra por conglomerados
A essência da amostra por conglomerados lembra um pouco a amostragem estratificada. Em ambos os casos nós dividimos a população em grupos. No entanto, os princípios posteriores das duas técnicas são opostos.
A amostragem estratificada é particularmente adequada quando os grupos (camadas) são internamente homogêneos e muito diferentes. Nesse caso, devemos garantir que temos representantes em nossa amostra que vêm de todos os estratos. Por outro lado, a amostragem por conglomerados é adequada quando os grupos que formam a população são muito semelhantes entre si, por isso não há grande diferença entre estudar indivíduos em um grupo ou de outro. É por isso que, embora ambas as técnicas dividem a população (estratos ou aglomerados), o processo de seleção dos indivíduos é radicalmente diferente.
Benefícios da amostra por conglomerados
- A principal vantagem desta técnica é a parte operacional: selecionar um conglomerado costuma ser mais fácil e mais barato do que fazer uma amostra aleatória ou sistemática. Usar clusters geográficos podem representar uma economia significativa no deslocamento.
- A principal desvantagem é o risco dos clusters não serem realmente homogêneos entre eles. No exemplo citado anteriormente, poderia acontecer de em uma das províncias ser mais propensas o número de fumantes por ser uma área mais urbana ou outras razões culturais.
Eficiência da amostra por conglomerados
Como podemos comparar esta técnica com as demais?
Normalmente essa relação poderá ser representada pelo coeficiente de correlação entre os conglomerados (δ), definido como o coeficiente de correlação linear entre todos os pares de valores das variáveis do estudo, medidos através das unidades dos conglomerados e estendido a todos os grupos. Em síntese, este coeficiente é uma medida de homogeneidade dentro de clusters.
Quanto menor o coeficiente de homogeneidade entre conglomerados δ, maior eficiência terá a amostragem por conglomerados. Vale lembrar que o ideal é que os conglomerados sejam heterogêneos como a amostra total, de modo que a seleção de um conglomerado nos forneça a mesma informação que a seleção dos indivíduos da população aleatória total.
Comparando a amostra aleatória simples com a amostragem por conglomerados, se δ =0 , podemos afirmar que os métodos são equivalentes. Esta condição implica que os clusters são tão heterogêneos como a população total. O pior caso seria δ=+1, e o caso mais favorável seria δ=-1/(M-1), onde M é o tamanho do conglomerado. No entanto, δ normalmente será sempre maior do que 0, pois um conglomerado sempre tem alguma semelhança uns com os outros.
Outra forma de ver o impacto deste problema é calcular o tamanho da amostra necessário para obter a mesma precisão de amostragem aleatória simples. Seria a expressão seguinte:
nc = na (1 + (M-1) δ)
Onde nc é o tamanho da amostra por conglomerado e na é o tamanho da amostra necessária para a amostragem aleatória simples. Portanto, (1+(M-1) δ é a variação do tamanho da amostra necessária devido ao uso de aglomerados. Normalmente, este será um incremento. Este fator é conhecido como efeito de desenho.
Esperamos que este post tenha sido útil para compreender melhor esta técnica de amostragem probabilística. Abaixo, você encontrará os artigos que compõem a série.
ÍNDICE: Série "Amostragem"
- Amostragem: O que é e por quê funciona
- Amostragem probabilística e não probabilística
- Amostragem probabilística: Amostar aleatória simples
- Amostragem probabilística: Amostra estratificada
- Amostragem probabilística: Amostra sistemática
- Amostragem probabilística: Amostra por conglomerados
- Amostragem não probabilística: Amostra por conveniência
- Amostragem não probabilística: Amostra por quotas
- Amostragem não probabilística: Amostra por bola de neve