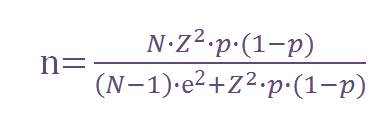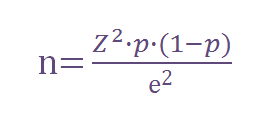Uma das sessões mais visitadas do nosso site é a CALCULADORA DE AMOSTRAS. Nesta página, indicando apenas alguns dados básicos sobre a população que se deseja investigar e o erro máximo que você está disposto a tolerar, obtém-se uma estimativa do tamanho da amostra necessária para a sua pesquisa.
Frequentemente recebemos dúvidas relacionadas a esta calculadora: quais fórmulas ela emprega, o que significa margem de erro, nível de confiança, etc. Hoje queremos explicar exatamente como tudo isso funciona.
O problema
O problema que queremos resolver é o seguinte: queremos estudar um universo de pessoas (por exemplo, brasileiros entre 15 e 65 anos, um total de 136 milhões de pessoas) através de uma pesquisa direcionada a uma amostra deste universo. Como a amostra tem um tamanho inferior ao total do universo, vamos acabar auferindo certo nível de erro nos dados que observarmos. Se estivermos dispostos a aceitar uma % de erro determinada, qual é o tamanho mínimo de amostra que eu precisaria entrevistar?
A forma como meço o erro
Quando quero fixar o erro máximo que estou disposto a aceitar em uma pesquisa, é comum nos referirmos a dois parâmetros: a margem de erro e o nível de confiança. O que cada um deles significa?
A margem de erro é o intervalo no qual espero encontrar o dado que quero medir do meu universo. O dado pode ser em geral de dois tipos: uma média ou uma proporção. Por exemplo, se eu quero calcular a média de filhos que os brasileiros entre 15 e 65 anos têm, quero poder dizer que a média é de 2,1 filhos/pessoa com uma margem de erro de 5%. Isso significaria que espero que a média esteja entre 2,1 – 5% e 2,1 + 5%, o que dá um intervalo de 2,00 <-> 2,21.
Se eu quisesse definir uma margem de erro para uma proporção, o processo seria o mesmo. Por exemplo, quero poder estimar o número de brasileiros entre 15 e 65 anos que têm casa própria, afirmando que são um total de 61,35 milhões de pessoas (45% da população) com uma margem de erro de 5%, isso significa que a realidade está entre 64,42 milhões (47,25%) e 58.28 milhões (42,75%).
O nível de confiança expressa a certeza de que o dado que buscamos realmente está dentro da margem de erro. Por exemplo, com base no caso anterior, se obtemos um nível de confiança de 95%, poderíamos dizer que a porcentagem de pessoas do meu universo que têm casa própria, em 95% dos casos se encontrará entre 42,75% e 47,25%. Ou seja, se eu repetir a minha pesquisa 100 vezes, selecionando amostras aleatórias do mesmo tamanho, 95 vezes a proporção que eu busco estaria dentro do intervalo e 5 vezes fora dele.
Relação entre o erro e o tamanho da amostra
Margem de erro, nível de confiança e tamanho da amostra sempre caminham lado a lado. Se eu quero obter uma margem de erro e um nível de confiança determinado (por exemplo, erro de 5% com confiança de 95%) precisarei de um tamanho de amostra mínimo correspondente. Modificar qualquer um dos 3 parâmetros, alterará os restantes:
1. Reduzir a margem de erro obriga a aumentar o tamanho da amostra.
2. Aumentar o nível de confiança obriga a aumentar o tamanho da amostra.
3. Se eu aumentar o tamanho da minha amostra, posso reduzir a margem de erro ou incrementar o nível de confiança.
Mas, quais fórmulas regem a relação entre os parâmetros anteriores? O conjunto de teoremas conhecidos como LEI DOS GRANDES NÚMEROS chega para nos salvar. Estes teoremas são os que dão suporte matemático à ideia de que a média de uma amostra aleatória de uma população grande tenderá a estar próxima da média da população completa. Sobretudo, o teorema do limite central mostra que, em condições gerais, a soma de muitas variáveis aleatórias independentes (no exemplo, os brasileiros que têm casa própria) «se aproximam bem» a uma distribuição normal (também chamada curva de Gauss).
Graças ao teorema do limite central, quando calculamos uma média (p.e. filhos por pessoa) ou uma proporção (p.e. % de pessoas com casa própria) de uma amostra, podemos saber qual é a probabilidade de que o universo tenha esse mesmo valor ou um valor parecido. O valor que calcularmos para a amostra será o mais provável para o nosso universo e conforme nos distanciamos deste valor (para cima ou para baixo) estes serão valores cada vez menos prováveis. No meu exemplo, se 45% da minha amostra de brasileiros têm casa própria, posso afirmar que 45% é o valor mais provável do universo estudado. Uma porcentagem de 44% será algo menos provável, 43% ainda menos, etc. O mesmo acontece para valores superiores: 46% é menos provável que 45%.
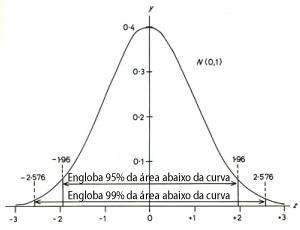
O fato da probabilidade diminuir conforme eu me distancio da média é o que caracteriza uma distribuição gaussiana. Podemos fixar um intervalo ao redor do valor mais provável, de forma a englobar 95% da probabilidade (nível de confiança). A distância que tenho que tomar a partir do valor mais provável para englobar estes 95%, determina a margem de erro.
Segundo o gráfico anterior, em uma distribuição normalizada (média 0, desvio padrão 1) se queremos englobar os valores que cobrem 95% dos casos, tenho que definir uma margem de erro entre -1,96 e +1,96 da média. Se eu quero cobrir 99% dos casos, a margem deve distanciar-se até +-2,58.
Então, o que a calculadora está fazendo?
Conhecendo a propriedade anterior, é muito fácil adaptar as fórmulas da distribuição gaussiana a qualquer caso (seja qual for a média e o desvio). Vamos ver com detalhes o caso da estimativa de uma proporção. Para tanto utilizaremos a seguinte fórmula:
Onde:
n = O tamanho da amostra que queremos calcular
N = Tamanho do universo (p.e. 136 milhões de brasileiros entre 15 e 65 anos)
Z = É o desvio do valor médio que aceitamos para alcançar o nível de confiança desejado. Em função do nível de confiança que buscamos, usaremos um valor determinado que é dado pela forma da distribuição de Gauss. Os valores mais frequentes são:
Nível de confiança 90% -> Z=1,645
Nível de confiança 95% -> Z=1,96
Nível de confiança 99% -> Z=2,575
e = É a margem de erro máximo que eu quero admitir (p.e. 5%)
p = É a proporção que esperamos encontrar. Este parâmetro tende confundir bastante à primeira vista: Como vou saber qual proporção espero, se justamente estamos fazendo uma pesquisa para conhecer esta proporção?
A razão pela qual esta proporção p aparece na fórmula é que quando uma população é muito uniforme, a convergência para uma população normal é mais precisa, permitindo reduzir o tamanho da amostra. Se no meu exemplo, eu espero que no máximo a % de pessoas que têm casa própria seja de 5%, eu poderia usar este valor como p e o tamanho da minha amostra reduziria. Se no entanto, eu não tenho ideia do que devo esperar, a opção mais prudente seria usar o pior cenário: a população se distribui em partes iguais entre proprietários e não proprietários, logo p=50%.
Como regra geral, usaremos p=50% se eu não tenho nenhuma informação sobre o valor que espero encontrar. Se eu tenho alguma informação, usarei o valor aproximado que espero (ajustando para 50% por via das dúvidas).
Podemos simplificar a fórmula anterior quando trabalhamos com universos de tamanhos muito grandes (se considera muito grande a partir de 100.000 indivíduos), resultando na seguinte fórmula:
Exemplo: Vamos retomar nosso caso anterior. Temos uma população de 136 milhões de brasileiros entre 15 e 65 anos, queremos saber qual a % deles tem casa própria, com uma margem de erro de 5% e um nível de confiança de 95%. Vamos supor que não temos nenhuma informação prévia sobre qual é a % de proprietários que podemos obter na pesquisa. Neste caso posso usar a fórmula simplificada, pois 136 milhões > 100.000, e usaremos p=50% pois não tenho informação prévia sobre o resultado esperado:
n = 1,96^2 * 0,5 * (1 – 0,5) / 0,05^2 = 384,16 -> 384
Devo, portanto, entrevistar 384 pessoas para manter-me dentro dos níveis de erro definidos.
Se em um estudo realizado no ano anterior obtivemos o resultado de que a % de brasileiros proprietários da casa própria era de 20%, e se espera que o dado deste ano não tenha variado em mais de 5 pontos (entre 15% e 25%), poderíamos substituir p pelo pior caso esperado = 25%. O resultado seria:
n = 1,96^2 * 0,25 * (1 – 0,25) / 0,05^2 = 288,12 -> 288
Tenho que fazer estes cálculos?
Não, por isso oferecemos uma calculadora que faz todo o trabalho por você. Você só precisa saber o valor do parâmetro “nível de heterogeneidade”, ou seja, qual é a proporção esperada mas, na ausência dessa informação, você pode indicar o valor de 50%.
Esperamos poder ter lhe ajudado a interpretar o uso dessa ferramenta.