Nate Silver , en La señal y el ruido, habla de las dificultades que afrontamos cuando tratamos de hacer buenas predicciones. Siguiendo la metáfora del título de su libro, la principal de ellas es confundir señal con ruido: desarrollamos un modelo predictivo y tratamos de ajustarlo a los datos que tenemos, pero, en el afán de afinar el modelo al máximo, acabamos ajustando el modelo a las imperfecciones de los datos que tenemos, empeorando nuestra capacidad predictiva.
Este fenómeno se conoce como over-fitting o sobreajuste. Un modelo predictivo debe capturar la esencia del fenómeno que describe, nada más. Christopher M. Bishop, en su libro Pattern Recognition and Machine Learning (Springer, 2006) nos ofrece un gran ejemplo de este problema, con un enfoque muy matemático (¡avisados estáis!).
¿Qué es un modelo?

Un modelo de datos es una expresión matemática que describe cómo se relacionan un conjunto de variables. Los modelos se crean y se ajustan a partir de un conjunto completo de datos, en los que tenemos todas las variables de interés. Una vez ajustado, el modelo es útil para poder predecir alguna de las variables a partir de la observación de otras.
Por ejemplo: podemos crear un modelo que relaciona el mes del año con la temperatura media diaria. Para crear y ajustar el modelo, podríamos observar datos de las temperaturas de los últimos 50 años. Una vez creado el modelo, podemos usarlo para predecir qué temperatura media puedo esperar que se produzca en un mes concreto durante el próximo año. En este caso, el mes sería la variable de entrada (x) y la temperatura la variable objetivo o variable predicha (t).
Dependiendo del fenómeno investigado, la relación entre variables de entrada y variables objetivo es más o menos fuerte. Esa relación define la capacidad predictiva del modelo. Rara vez un modelo puede describir por completo un fenómeno, lo que sería un modelo determinista: lo habitual es que las predicciones sean imperfectas.
Por ejemplo, los modelos meteorológicos toman como variables de entrada la temperatura, humedad, presión atmosférica y otros datos similares para predecir la temperatura futura y la probabilidad de lluvia. Los modelos meteorológicos no son infalibles. Cuando el modelo trata de predecir el tiempo con más días de antelación, más puede fallar.
Datos sintéticos
Bishop nos propone un interesante ejercicio para explicar el over-fitting. Para ello, crea una relación artificial entre una variable de entrada x y una variable objetivo t, lo que permite crear datos sintéticos. Posteriormente, trata de diseñar un modelo que describa esos datos sin usar información de cómo han sido creados.
Para crear los datos sintéticos, Bishop usa una función conocida, t=sin(2πx), a la cual añade un poco de ruido, sumando a la variable t una cierta cantidad aleatoria. Usando este método, generamos un conjunto de datos formado por 10 valores de x uniformemente distribuidos entre 0 y 1 con sus correspondientes valores de t. El siguiente gráfico muestra estos datos:
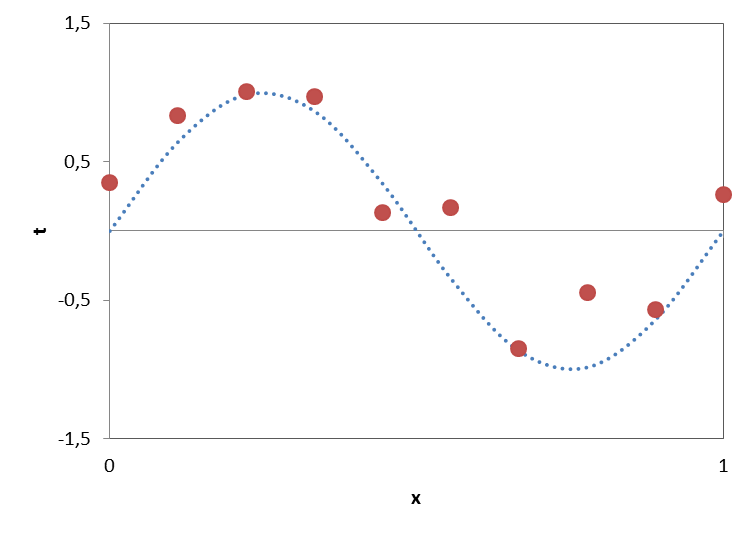
Los puntos rojos son las parejas de valores (x,t). La línea azul discontinua muestra la función sin(2πx) usada para generar los datos. La distancia entre los puntos rojos y la línea discontinua es el ruido aleatorio que hemos añadido.
La forma en que hemos generado estos datos captura una propiedad muy habitual de los datos que encontramos en problemas reales: poseen una regularidad subyacente, que es la que queremos capturar y modelizar, pero al observar un conjunto individual de datos estos se ven corrompidos por algún tipo de ruido aleatorio. Este ruido puede surgir por la propia naturaleza aleatoria del proceso, pero lo más habitual es que se deba a que no estamos observando alguna fuente de variabilidad que afecta al fenómeno estudiado.
Un modelo para nuestros datos
Supongamos que observamos únicamente los puntos rojos y que desconocemos que provienen de una función sinusoidal. Nuestro propósito es crear un modelo, ajustarlo (entrenarlo) con los datos que tenemos (las 10 parejas de valores de x y t descritos por los puntos rojos) con el objetivo de poder predecir para nuevos valores de x, qué valores de t vamos a observar.
Este objetivo es ambicioso: en realidad lo que queremos es descubrir la función sin(2πx) a partir de un conjunto limitado de datos (10 puntos) y corrompidos (debido al ruido).
Para diseñar nuestro modelo vamos a usar una técnica conocida como ajuste de curvas (curve fitting). En concreto, trataremos de ajustarnos a los datos usando una función polinómica como la siguiente
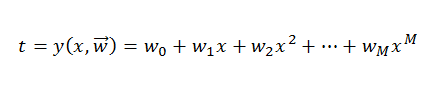
donde M es el orden del polinomio y xj es el valor de x elevado la potencia j. Los parámetros w0 ,w1 ,...,wM los podemos referenciar de forma agupada como un vector w⃗.
Ajustar el modelo (entrenarlo)
Una vez hemos definido la estructura de nuestro modelo, tenemos que entrenarlo con los datos que tenemos (en este caso, los 10 puntos rojos). El objetivo es encontrar los valores de los parámetros w0 ,w1 ,...,wM que mejor relacionan x y t.
Esto se puede hacer minimizando una función de error. Una elección habitual es usar el error cuadrático, la suma de los cuadrados de la diferencia entre el valor t observado y el valor de t estimado por nuestra función y(x,w). Es decir, queremos minimizar la siguiente función:
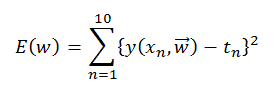
Esta forma de calcular el error tiene buenas propiedades: cuanto más distancia hay entre el modelo y los datos, mayor es el error. Y el error sólo es cero si nuestra curva pasa exactamente por los puntos rojos.
Minimizar la función de error anterior es simple, dado que es una función cuadrática de los parámetros w, de manera que las derivadas respecto a los parámetros son funciones lineales. Por lo tanto, podemos encontrar una solución única, un conjunto de parámetros que llamaremos w*.
Complejidad del modelo
Sin embargo, queda una cuestión pendiente: ¿qué orden M escogemos para el polinomio empleado en el modelo? Ésta es una cuestión clave, que se conoce como selección del modelo (model selection). Cuanto mayor sea M, más parámetros podemos ajustar y más flexible es nuestro modelo. Un modelo más flexible se puede ajustar más a los datos.
Un modelo con M=0 es simplemente una constante, y=w0. Un modelo con M=1, es una recta, y=w0+w1x. Con M=2 tenemos una parábola, etc.
Veamos el resultado de ajustar el modelo usando M=0,1,3 y 9.
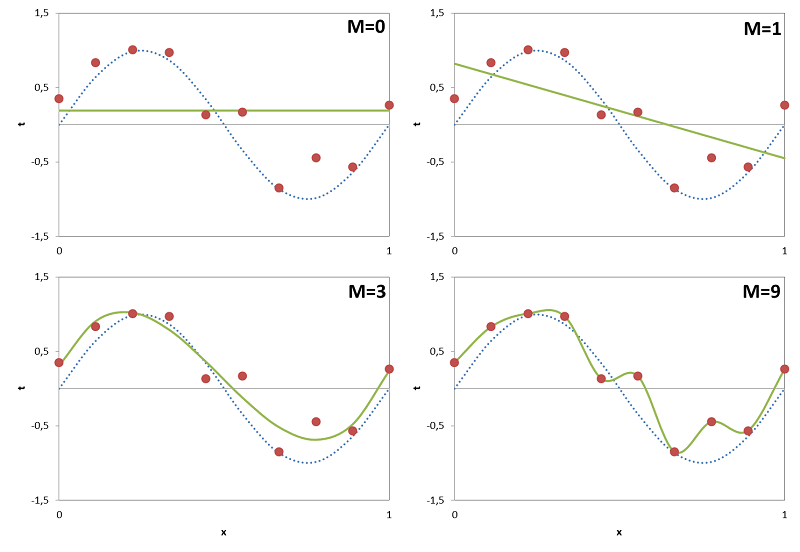
Mirando los resultados, vemos que los modelos con M=0 y M=1 se ajustan muy mal a los datos que queremos reproducir: son demasiado rígidos. El modelo con M=3 reproduce bastante bien los datos (aunque la curva no pasa exactamente por los puntos rojos). Curiosamente, tiene una forma muy similar a la función sin(2πx). Parece que un modelo con este nivel de complejidad captura la esencia de los datos que queremos describir.
Si seguimos añadiendo complejidad al modelo y usamos M=9 (10 parámetros), se produce la paradoja: el modelo se ajusta perfectamente a los datos (la curva pasa por los puntos rojos) y por lo tanto no tiene error. Sin embargo, a simple vista se observa que la curva no sigue el patrón de la función subyacente sinusoidal, es una curva errática que va siguiendo los puntos rojos.
Nos encontramos con un caso de over-fitting o sobreajuste. Hemos ajustado el modelo al ruido de los datos, en lugar de ajustarlo a la natualeza del fenómeno que queremos modelizar.
¿Cuándo tenemos riesgo de over-fitting?
En el ejemplo que hemos mostrado vemos que un modelo más simple – y por lo tanto menos flexible – es capaz de reproducir mejor la esencia de lo que queremos representar. Usar modelos demasiado complejos puede hacer que demos demasiada importancia al ruido en lugar de a la señal.
Decidir el grado de complejidad de un modelo requiere mucha experiencia. Os recomiendo la lectura del libro en el que se inspira este ejemplo, pero es posible dar facilitar algunas ideas al respecto.
La primera es que debe existir un equilibrio entre la cantidad de datos que tenemos y la complejidad del modelo. En nuestro ejemplo, cuando usamos un modelo con 10 parámetros para describir un problema para el que tenemos 10 datos, el resultado es previsible: vamos a construir un modelo a medida de los datos que tenemos, estamos resolviendo un sistema de ecuaciones con tantas incógnitas como ecuaciones. Dicho de otra manera: si este modelo con 10 parámetros lo hubiésemos ajustado con un total de 100 datos en lugar de 10, seguramente funcionaría mejor que un modelo más básico.
La segunda idea básica: otra forma de detectar que nuestro modelo padece over-fitting es observar el valor de los parámetros. Cuando se produce over-fitting, los parámetros de nuestro modelo crecen de forma desmesurada, haciendo oscilar nuestra curva abruptamente. De hecho, una manera de evitar el over-fitting sin necesidad determinar manualmente la complejidad del modelo es añadir a la función de error que queremos minimizar la suma de los cuadrados de los parámetros. De esta forma penalizamos los modelos más complejos, promoviendo que los parámetros sean más suaves.
La prueba definitiva: la generalización
Finalmente, la mejor manera de evaluar si un modelo funciona es… ¡probarlo con nuevos datos! A fin de cuentas, si creamos un modelo es para poder predecir resultados.
Para probar un modelo lo que se suele hacer es obtener un conjunto de datos diferente al que se ha empleado para entrenar el modelo (a veces se dividen los datos disponibles en dos grupos, unos para ser usados en la fase de entrenamiento del modelo y otros para la fase de test). Si el modelo funciona, deberíamos obtener buenas estimaciones de la variable objetivo a partir de los nuevos datos.
Veamos qué sucede en el ejemplo anterior si obtenemos 10 nuevos datos y comparamos los valores de t con las predicciones del modelo que hemos creado. Si hacemos esta comparación para cada posible complejidad del modelo (número parámetros del modelo), obtenemos el resultado siguiente.
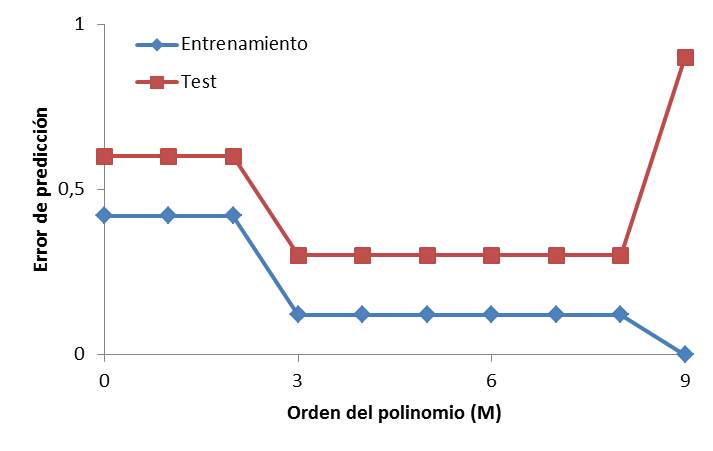
El gráfico muestra como en fase de entrenamiento, cuantos más parámetros usamos en el modelo, menor error cometemos, hasta llegar a M=9 (10 parámetros), momento en el que el error es nulo: el modelo se ajusta totalmente a los datos.
Al validar el modelo frente a nuevos datos de test, vemos que el error es algo mayor en general pero que evoluciona de igual manera: mayor número de parámetros, menor error. Sin embargo, observamos dos cosas importantes: (1) a partir de M=3, la mejora del error es muy pequeña, lo que indica que el modelo es suficientemente bueno. Y (2) cuando llegamos a M=9, el error se dispara: tenemos un modelo sobre-ajustado a los datos de entrenamiento y al emplearlo en un conjunto nuevo de datos, falla estrepitosamente.
Cuando este problema sucede decimos el modelo no está “generalizando” bien. Como no ha capturado la información esencial del problema estudiado, no es capaz de dar buenas predicciones cuando le damos nuevos datos generales.
Lecciones para todo investigador
Con el crecimiento imparable de las capacidades de computación y la mejora de los softwares de análisis es tentador crear modelos muy sofisticados. Mayor sofisticación no siempre implica mayor precisión: debemos seleccionar bien qué variables usamos en nuestro modelo y ajustar bien la complejidad del mismo a la cantidad de datos que tenemos. Sólo así haremos predicciones de la señal, y no del ruido.






