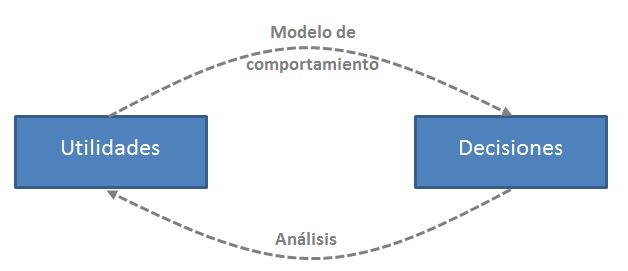
Podemos analizar un Conjoint de diferentes maneras. Cada una de ellas se basa en un modelo de comportamiento: una forma matemática de describir cómo deciden las personas. El modelo más simple es el modelo Logístico Multinomial.
Cómo se analiza un Conjoint
El análisis Conjoint siempre sigue el siguiente proceso:
- Definimos un modelo de comportamiento que relaciona las utilidades de los productos con las decisiones de las personas. Este modelo permite predecir, a partir de las utilidades, la probabilidad de que un individuo elija un producto entre varios disponibles.
- El análisis consiste en hacer el camino contrario. Viendo las decisiones de las personas frente a unos productos, buscamos las utilidades que explican mejor las decisiones que hemos observado.
El modelo logístico multinomial (MNL)
En este post veremos el modelo más simple empleado para análisis Conjoint, el modelo logístico multinomial (MNL – MultiNomial Logistic). Este modelo acepta unas hipótesis bastante restrictivas que, a cambio, hacen que el análisis sea extremadamente simple. Piensa que el modelo fue desarrollado en los años 70, en una época en la que los ordenadores no tenían la capacidad de cálculo actual. Disponer de un modelo simple era una ventaja crucial.
Hipótesis del modelo MNL
Todo modelo de comportamiento asume unas hipótesis sobre los respondientes y la forma en que se comportan. El modelo MNL se basa en las siguientes hipótesis:
- El error en las estimaciones de utilidad sigue una distribución de probabilidad tipo valor extremo: Esta distribución es similar a la normal – la probabilidad es máxima en un valor central y decrece rápidamente cuando nos alejamos - pero se describe mediante una función integrable. Esta hipótesis simplifica las expresiones matemáticas del modelo.
- La parte de la utilidad que no observamos está incorrelada entre atributos: Es una hipótesis un poco técnica, pero importante. En el modelo MNL estamos suponiendo que hay unos factores que no estamos considerando pero que afectan al respondiente y que son la causa de que nuestra estimación de utilidad no sea perfecta. Los factores no observados son el origen del error de estimación. Pues bien, la hipótesis que debemos aceptar es que no hay correlación en la forma en que estos factores no observados afectan a unos y otros atributos. Dicho de otra forma, tener mucho error en un atributo debería ser independiente de tener error en otro atributo.
- Independencia de alternativas Irrelevantes (IAI). A consecuencia de la hipótesis anterior, el modelo MNL nos dice que la probabilidad relativa de elegir una opción A frente a otra opción B no cambia por la presencia o ausencia de otras opciones (son alternativas irrelevantes). La hipótesis de IAI es el fundamento de muchos modelos de decisión, pero ha sido cuestionada por varios estudios psicológicos que muestran que el ser humano no siempre decide así.
Un ejemplo: el famoso problema del autobús rojo – autobús azul. Un viajero tiene la opción de ir al trabajo en automóvil o en un autobús azul. Supongamos que la utilidad de los dos medios de transporte es la misma, de tal manera que las probabilidades de elección son iguales: Pcoche=Pbus_azul=1/2. En este caso, el ratio de probabilidades es uno: Pcoche/Pbus_azul=1.
Ahora imagina que se introduce una nueva opción de transporte, un autobús rojo, y que el viajero considera que el autobús rojo es exactamente igual que el autobús azul. La probabilidad de que el viajero elija el autobús rojo es por lo tanto la misma que para el autobús azul, de manera que el ratio de sus probabilidades es uno: Pcoche/Pbus_azul=1. Sin embargo, el modelo MNL exige que el ratio Pcoche/Pbus_azul siga siendo el mismo (1), haya o no una nueva alternativa. Las únicas probabilidades de elección que respetan ambas condiciones son Pcoche=Pbus_azul=Pbus_rojo=1/3, que son justamente las probabilidades que el modelo MNL predice.
No parece una buena predicción… En el mundo real, sería de esperar que la probabilidad de que el viajero eligiese el automóvil se mantuviese igual cuando un nuevo autobús exactamente igual al ya existente estuviese disponible. Es decir, esperaríamos una solución Pcoche=1/2 y Pbus_azul=Pbus_rojo=1/4. En un caso así el modelo MNL falla, aunque ciertamente es un caso excepcional.
- Todos los individuos perciben la misma utilidad de un atributo. El modelo MNL no admite variación aleatoria de preferencias entre individuos. ¿Qué quiere decir esto? Quiere decir que dos personas idénticas no pueden tener preferencias diferentes. Toda diferencia tiene que venir explicada por un factor objetivo, esté o no esté en el modelo.
Pero, si todos los individuos iguales perciben igual utilidad de los atributos, ¿cómo explica el modelo que no todos ellos respondan igual el cuestionario Conjoint? Para el modelo MNL las diferencias en sus respuestas se deben a factores que no estamos observando y que generan error de estimación.
Esta hipótesis puede parecer muy limitante, pero no lo es tanto. En la práctica puedes ver el asunto de una manera más simple: el modelo MNL estima para cada atributo la utilidad media en la población. Es por ello que nos referimos a un modelo de análisis agregado, no individual.
Probabilidad de elección MNL
Hemos dicho que un modelo de comportamiento nos permite predecir qué van a elegir las personas a partir de la utilidad de los productos. Veamos cómo funciona esta relación en el modelo MNL.
Supongamos que un individuo debe elegir entre 4 productos diferentes. Imaginemos que conocemos la utilidad de esos 4 productos: U1, U2, U3 y U4. El modelo MNL prevé una probabilidad de que el decisor elija la primera opción de:
P<sub>1</sub> = e<sup>U1</sup> /( e<sup>U1</sup>+ e<sup>U2</sup>+ e<sup>U3</sup>+ e<sup>U4</sup>)
Para el resto de opciones, las probabilidades serían equivalentes. Como puedes ver, es una expresión sencilla, sólo tenemos que exponenciar las utilidades (“e” es el operador exp() de Excel). Esta fórmula es muy simple gracias a que hemos considerado que el error de estimación sigue una distribución tipo valor extremo.
Veamos un ejemplo. Imagina que hemos estimado la utilidad que tienen dos atributos con dos niveles en un estudio Conjoint sobre coches:
Atributo 1 = Color.
-
Blanco -> U<sub>blanco</sub>=-0,5
-
Negro-> U<sub>negro</sub>=0,2
Atributo 2 = Marca.
-
VW -> U<sub>vw</sub>=1,2
-
Renault-> U<sub>renault</sub>=0,8
Si queremos predecir qué probabilidad hay de que un comprador elija uno de los 4 posibles coches que resultan de estos atributos (suponiendo que estuviese forzado a comprar una de las 4 opciones), deberíamos realizar la siguiente operación.
- Calcular las utilidades de las diferentes opciones como suma de las utilidades de los atributos que las componen.
Coche 1, VW Blanco à U1 = U<sub>vw</sub> + U<sub>blanco</sub> =1,2-0,5=0,7
Coche 2, VW Negro à U1 = U<sub>vw</sub> + U<sub>negro</sub> =1,2+0,2=1,4
Coche 3, Renault Blanco à U1 = U<sub>renault</sub> + U<sub>blanco</sub> =0,8-0,5=0,3
Coche 4, Renault Negro à U1 = U<sub>renault</sub> + U<sub>negro</sub> =0,8+0,2=1,0
- Evaluar las probabilidades de las opciones
P<sub>coche1</sub>= e<sup>U1</sup> /( e<sup>U1</sup>+ e<sup>U2</sup>+ e<sup>U3</sup>+ e<sup>U4</sup>)= e<sup>0,7</sup> /( e<sup>0,7</sup>+ e<sup>1,4</sup>+ e<sup>0,3</sup>+ e<sup>1,0</sup>)=20%
P<sub>coche2</sub>= e<sup>1,4</sup> /( e<sup>0,7</sup>+ e<sup>1,4</sup>+ e<sup>0,3</sup>+ e<sup>1,0</sup>)=40%
P<sub>coche3</sub>= e<sup>0,3</sup> /( e<sup>0,7</sup>+ e<sup>1,4</sup>+ e<sup>0,3</sup>+ e<sup>1,0</sup>)=13%
Pcoche4= e1,0 /( e0,7+ e1,4+ e0,3+ e1,0)=27%
Ya tenemos una fórmula que nos permite predecir en qué proporción se elegirá un producto a partir de su utilidad y la de sus competidores. Es decir, el market share entre compradores.
Y el análisis, ¿cómo se hace?
Ya sabemos pasar de utilidades a probabilidades. Pero lo que queremos hacer es lo contrario. Piensa qué tipo de información obtenemos en una encuesta Conjoint. Las respuestas de los participantes son elecciones (=decisiones) frente a un oferta de dos o más productos. Si pedimos a 100 personas que elijan entre la opción A y la B, y 20 optan por la A, podemos inferir que el 20% de la población prefiere A frente a B.
Pues bien, ese % de gente que ha optado por A frente a B es equivalente a la probabilidad de elección de A frente a B. Viéndolo así, la tarea de análisis será buscar las utilidades de A y de B que predigan una probabilidad de elección de A frente a B del 20%.
Parece fácil, pero no lo es tanto. A y B son productos compuestos por varios atributos, y es la utilidad de esos atributos lo que tenemos que encontrar. Y esos atributos se combinarán de diferentes formas para formar productos C, D, E, etc. cuyas probabilidades de elección estimadas tendremos gracias a la encuesta Conjoint. Al final, la encuesta nos dará datos de muchas elecciones respecto a múltiples combinaciones de atributos.
¿Cómo podemos encontrar utilidades que cuadren con todas las elecciones de los encuestados a la vez?
La respuesta es que no podemos lograrlo. Pero sí podemos lograr estimar las utilidades que se equivoquen lo menos posible en la predicción. Para hacerlo, lo habitual es usar el siguiente método:
- Partimos de unas utilidades iguales para todos los atributos.
- Calculamos las probabilidades de elección para cada situación de elección de la encuesta.
- Calculamos el error cometido entre nuestra predicción y las respuestas de la encuesta.
- Modificamos las utilidades de la forma que más reduzcan el error.
- Repetimos los pasos 2-4 hasta que no logremos reducciones apreciables en el error.
El análisis mediante el modelo Logit Multinomial es una forma simple de analizar un Conjoint, pero sólo nos permitirá obtener conclusiones a nivel agregado. Podremos hablar de las preferencias de la muestra, pero no de las preferencias de un individuo o grupo de individuos concreto. En el próximo post, veremos un método más sofisticado que nos será de mucha ayuda.
¿Te ha gustado el post? ¿Quieres profundizar más sobre el tema? Pues hemos preparado una serie de diez cápsulas sobre Conjoint. ¡No te pierdas ninguna!
ÍNDICE: Serie Cápsulas sobre Conjoint
Cápsula 1: Qué es un estudio Conjoint y cómo utilizarlo
Cápsula 2: Entendiendo el concepto de utilidad
Cápsula 3: Fases de un Conjoint
Cápsula 4: Diseño experimental, parámetros de diseño
Cápsula 5: Diseño experimental, calidad de un diseño
Cápsula 6: Diseño experimental y estrategias para encontrar un buen diseño
Cápsula 7: Programación de cuestionarios Conjoint
Cápsula 8 - Análisis agregado de un Conjoint
