Hace unos días publicábamos un post acerca de la confrontación entre dos formas de entender la estadística: el pensamiento Frecuentista (o clásico) y el pensamiento Bayesiano. Los primeros entienden la probabilidad como el resultado esperado de un experimento repetible, los segundos como el grado de conocimiento que tenemos acerca de la posibilidad de que un evento ocurra.
El pensamiento Bayesiano está en el corazón de muchos de los grandes avances de la estadística moderna. Uno de sus usos más curiosos tiene que ver con la justicia. El teorema de Bayes es una buena manera de valorar objetivamente la culpabilidad de un acusado. Por lo menos, así había sido hasta hace poco.

La sentencia de un juez británico
Hace unos años saltó una sorprendente noticia sobre el uso de la estadística en los juicios. Un juez británico decidió que el teorema de Bayes, una fórmula frecuentemente empleada para determinar la probabilidad de que un acusado sea culpable, no debía usarse en casos de homicidio. O por lo menos, no como se venía haciendo.
Este famoso teorema permite evaluar la probabilidad de un suceso en dos pasos. En primer lugar, parte de una probabilidad a priori, una estimación de que un determinado evento ocurra basándonos en nuestro conocimiento previo del problema. En segundo lugar, una vez hemos podido adquirir nuevos datos que mejoren nuestro conocimiento del problema, calculamos una probabilidad posterior. Esta probabilidad posterior es el resultado de revisar nuestras creencias a priori sobre la base de las evidencias disponibles.
Según el juez británico, cualquier testigo experto que aplique este teorema para evaluar las probabilidades de que un acusado sea culpable, debería tener una certeza total sobre los datos estadísticos que emplea.Esta decisión podría afectar al uso actual de este teorema para determinar coincidencias en rastros de drogas, fibras de tejidos de una prenda de vestir o huellas, quedando únicamente las pruebas de ADN a salvo de esta sentencia.
El detonante de esta decisión judicial es un caso real de asesinato juzgado en Reino Unido. El sospechoso fue condenado después de que se hallase en su domicilio unas zapatillas deportivas Nike que coincidían con unas huellas encontradas en la escena del crimen. El razonamiento bayesiano que el testigo experto realizó en este caso necesitaba asignar una probabilidad al hecho de que una persona cualquiera llevase dicho modelo de zapatillas deportivas. Ante la ausencia de datos precisos por parte del fabricante, el experto empleó una estimación razonable de esta información, una práctica habitual en este tipo de razonamientos. Por lo visto, al juez no le gustó la idea de condenar a alguien con base a una estimación de este tipo.
Cómo se usa el teorema de Bayes en los juicios
Veamos cómo se usa el teorema de Bayes en la incriminación de acusados. Empecemos recordando el célebre teorema en su formulación más habitual.
Extra expresión relaciona la probabilidad de que ocurran dos eventos A y B. Cada elemento de esta fórmula debe entenderse de la siguiente manera:
- P(A) = Probabilidad de que ocurra un evento A.
- P(B) = Probabilidad de que ocurra un evento B.
- P(A|B) = Probabilidad de que ocurra el evento A, sabiendo que ha ocurrido el evento B. Se lee como probabilidad condicionada de A respecto a B.
- P(B|A) = Probabilidad de que ocurra el evento B, sabiendo que ha ocurrido el evento A. Es decir, probabilidad de B condicionada a A.
La noción de probabilidad condicionada es fundamental en la estadística y nos permite tener en cuenta eventos relacionados entre sí. Por ejemplo, la probabilidad de que un día cualquiera resbale paseando por la calle puede ser de 1 entre 1.000, pero esa misma probabilidad condicionada a que ese día esté lloviendo puede ser de 1 entre 100.
En ocasiones, en lugar de emplear probabilidades, empleamos lo que los ingleses llaman odds, que es el número de veces que ocurrirá un evento respecto al número de veces que ocurrirá otro. Dicho de otra manera, O(A)=P(A)/P(no A).
Supongamos que el evento A es la culpabilidad del acusado (le llamaremos Culp) y el evento B la aparición de una evidencia inculpatoria (E a partir de ahora). En dicho caso, P(Culp|E) debería leerse como la probabilidad de que el acusado sea culpable habiendo observado una evidencia del delito. Teniendo en cuenta este concepto, es frecuente transformar la fórmula anterior de manera más conveniente para nuestro propósito:
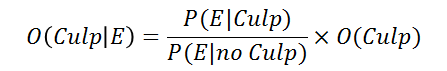
Debemos leer cada elemento de la fórmula así.
- O(Culp) = Probabilidad de que el acusado sea culpable respecto a la probabilidad de que sea inocente, antes de observar ninguna prueba o evidencia.
- O(Culp|E) = Probabilidad de que el acusado sea culpable una vez hemos observado una evidencia E, respecto a la probabilidad de que sea inocente.
- P(E|Culp) = Probabilidad de que se produzca la evidencia E cuando el sospechoso es culpable.
- P(E|no Culp) = Probabilidad de que se produzca la evidencia E cuando el sospechoso es inocente.
Lo interesante de la fórmula anterior es que, desde un punto de vista bayesiano, se puede leer como una revisión del grado de conocimiento que tenemos de un problema. Podemos pensar que O(Culp) son las opciones que damos al acusado de ser culpable sin tener ninguna prueba contra él y O(Culp|E) es la revisión de nuestra creencia acerca de su culpabilidad en vista de las evidencias aportadas.
Veamos cómo funciona este razonamiento con un ejemplo.
Ejemplo de revisión de probabilidad a priori
Supongamos que investigamos un homicidio en el que tenemos un sospechoso. Supongamos también que el homicida fue herido durante el acto y se han encontrado restos de su sangre en la escena del crimen. Un análisis forense determina que 1 de cada 15.000 personas tienen ese perfil sanguíneo y que coincide con el perfil de nuestro sospechoso. Por lo tanto
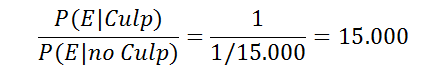
En la fórmula anterior, usamos probabilidades condicionadas. Si el acusado es culpable, la probabilidad de que la sangre encontrada sea del tipo observado es 1. Si es inocente, la probabilidad es la frecuencia con la que ese tipo de sangre se encuentra en la población general (1 de cada 15.000 veces).
Para poder usar nuestra fórmula, nos falta conocer las opciones de culpabilidad a priori que asignamos al sospechoso, sin tener en cuenta las pruebas de sangre. Supongamos que estamos en una región de 2.000.000 de personas y aceptamos que el culpable debe vivir necesariamente en ella. Podemos estimar que las opciones de culpabilidad a priori de nuestro acusado son de 1 contra 1.999.999.
Usando el teorema de Bayes revisamos estas opciones de culpabilidad con la evidencia de la prueba sanguínea
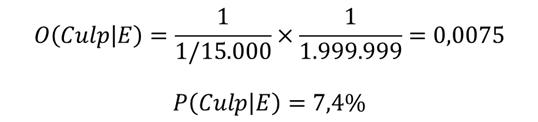
En el cálculo anterior hemos transformado las opciones de culpabilidad en probabilidad directa de culpabilidad, sabiendo que O= P / (1 - P), y por tanto P = O/(1+O).
El resultado puede parecer sorprendente. La prueba de la sangre incrementa por un factor 15.000 las opciones de culpabilidad del acusado, pero como sus opciones a priori eran bajas, sólo logramos tener una certeza de culpabilidad del 7,4%.
Para entender el impacto de la probabilidad a priori, supongamos ahora que el crimen ocurre en una región aislada de 2.000 habitantes. ¿Cómo afecta este conocimiento a priori a nuestra probabilidad de culpabilidad? Podemos modificar nuestra estimación, considerando esta vez que las opciones a priori de culpabilidad son 1 entre 2.000.
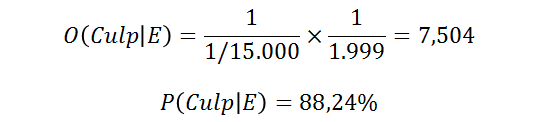
Pasamos a tener una certeza del 88%, muy superior a la anterior.
Los jurados nos son matemáticos
El razonamiento bayesiano es una herramienta poderosa. Pero, tal y como el juez británico apuntó, es muy sensible a las probabilidades a priori que usamos cuando no tenemos datos sólidos en qué basarnos.
En el fondo de la cuestión está el hecho de que la justicia no se siente cómoda asignando probabilidades a la cuestión de la culpabilidad. Uno de los principios básicos del derecho en la mayor parte de culturas es que no se puede condenar a una persona cuando hay alguna duda de su culpabilidad (in dubio pro reo). Pero en realidad, rara vez podemos tener una certeza total sobre las cosas. El pensamiento Bayesiano pone en evidencia esta realidad. Sin embargo la sociedad necesita dormir tranquila pensando que no enviamos inocentes a la cárcel. El teorema de Bayes es una verdad incómoda para el sistema jurídico.
Asimismo, es importante tener en cuenta cómo se interpretan estos conceptos por parte de un jurado sin perfil estadístico. La prueba sanguínea anteriormente mencionada, que afirmaba que 1 de cada 15.000 personas tiene un perfil sanguíneo similar, puede ser fácilmente mal interpretada. Si invertimos inadecuadamente el razonamiento, podemos pensar que el acusado sólo tiene 1 entre 15.000 opciones de ser inocente. Sin embargo, una cosa no tiene nada que ver con la otra.
Una correcta aplicación del teorema de Bayes proporciona indudables beneficios a la forma en que juzgamos en nuestra sociedad. Sería una pena perderlos.






