Una de las secciones de nuestra web más visitadas es la calculadora de muestras: una aplicación online que te indica cuantas personas deberías encuestar para estimar un dato de una población sin superar un nivel máximo de error.
A menudo recibimos consultas acerca de qué hace esta calculadora: qué fórmulas emplea, qué significan términos como margen de error o nivel de confianza. Hoy te explicamos cómo funciona exactamente y qué tamaño muestral necesitas para abordar una investigación.
El problema
Imagina que quieres saber qué porcentaje de la población brasileña entre 15 y 65 años fuma. O cuantos minutos por día ven la televisión. Obviamente, lo ideal sería preguntar a todos los miembros de la población (136 millones) pero eso es extremadamente costoso. Por ello normalmente optamos por encuestar a una parte de la población, lo que se conoce como una muestra. Como una muestra no contiene a todos los individuos, inevitablemente vamos a cometer cierto error en nuestras estimaciones. Cuanto más pequeña sea la muestra, ese error va a ser potencialmente mayor.
Pero ¿es posible asegurar que el error de estimación no supere ciertos límites? Sí, es posible y vamos a ver cómo.
Un poco de teoría: el teorema central del límite
Para empezar, simplifiquemos un poco el problema. La población brasileña entre 15 y 65 años es muy grande, podemos considerarla una población infinita. Esta asunción es muy práctica: permite aceptar que cada vez que selecciono un individuo para mi muestra, su probabilidad de tener la característica que quiero medir (por ejemplo, fumar) es constante, con independencia de los individuos que ya haya seleccionado anteriormente. Veremos luego qué hacer si no puedo aceptar la asunción de población infinita.
Si aceptamos esta simplificación, podemos utilizar el teorema central del límite. Este teorema dice que si obtenemos múltiples muestras de \( n \) individuos de una población infinita, la media de estas muestras tiende a una distribución Normal centrada en la media de la población. Y dice algo más: esta distribución Normal tiene una desviación típica igual a la desviación de la población de origen dividida por \( \sqrt{n} \).
Veamos qué significa esto en la práctica. Volvamos a la población brasileña, a los 136 millones. Imagina por un momento que pudiésemos observar a todos los individuos y medir cuánto tiempo ven la televisión. Unos la verán poco, otros mucho… pero con todos los individuos podríamos calcular una media exacta (supongamos 400 minutos). También podríamos calcular la desviación típica de la población, una medida de la dispersión de los individuos respecto a la media (por ejemplo, 100 minutos).
Ahora supongamos que obtenemos una muestra aleatoria simple de \( n \) personas y observamos cuánto ven la TV. La media en esta primera muestra debería ser similar a la media de la población (400), pero seguramente no será exacta. Podría ser 380, por ejemplo. A continuación, obtenemos un segundo tamaño muestral y resulta una media de 415. Y una tercera, y una cuarta… Y así sucesivamente. La secuencia podría ser algo así.
Muestra 1 -> Media observada 380
Muestra 2 -> Media observada 415
Muestra 3 -> Media observada 405
Muestra 4 -> Media observada 394
...
Lo que nos dice el teorema central del límite es que estas medias que observamos en las muestras de \( n \) individuos forman a su vez una distribución de probabilidad Normal. La media de esta distribución de medias coincide con la media de la población original, que llamaremos \( \mu \) . Y la desviación de esta distribución de medias es igual a la desviación original (que llamaremos \( \sigma \) ) dividida por \( \sqrt{n} \) . Es decir, \( \sigma / \sqrt{n} \) .Y esta es la razón por la que cuanto mayor es el tamaño de una muestra, más precisa es la estimación: la distribución de medias está más concentrada en torno a la media de la población y por lo tanto es más probable que la media de la muestra se acerque a la media de la población.
El siguiente esquema te puede ayudar a entender el teorema central del límite.
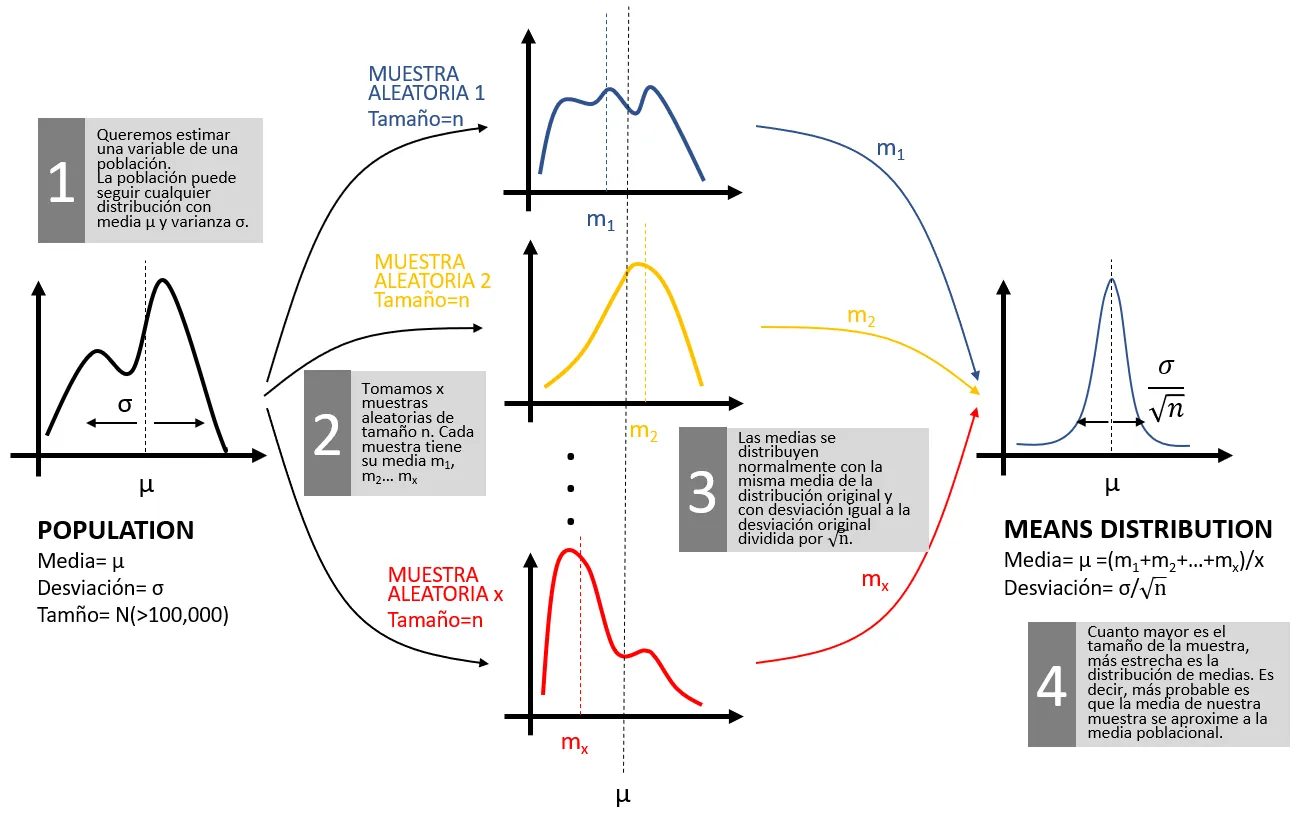
El teorema central del límite funciona aunque la población original no se distribuya de forma Normal. Se cumple para cualquier distribución. Al final, las medias de las muestras sí se distribuyen de forma Normal. Y esto es lo que nos permite medir y acotar el error de nuestras estimaciones.
Te puede interesar: Cuestionario y encuesta: ¿Cómo se Diferencian?, ¿Qué es una encuesta?, ¿Qué es una encuesta por muestreo? , Muestreo, qué es y por qué funciona, Tipos de items en las encuestas online.
Margen de error y nivel de confianza
Ya sabemos qué podemos esperar si obtenemos muchas muestras de nuestra población. Pero en la práctica, solo tenemos una muestra de tamaño \( n \) . Sin embargo, saber que esta muestra forma parte de una distribución de medias nos sirve de ayuda.
Una distribución Normal tiende a estar concentrada en torno a la media. Y sabemos en qué medida. Por ejemplo, sabemos que en el 90% de los casos, la media de la muestra va a estar en un intervalo \( \mu \pm 1.645 \cdot \sigma / \sqrt{n} \). O que en el 95% de los casos, la media va a estar en un intervalo \( \mu \pm 1.96 \cdot \sigma / \sqrt{n} \).
La relación entre “el 90% de los casos” (conocido como el nivel de confianza) y el valor “1.645”(conocido como Z-score) es una propiedad de la distribución Normal. Podemos fijar otros niveles de confianza. Habitualmente se usan niveles de confianza (NC) de 80%, 90%, 95% y 99%, a los que corresponde los Z-scores 1.282, 1.645, 1.960 y 2.576.
|
Nivel de confianza (NC) |
Z-score
|
| 80% | 1.282 |
| 90% | 1.645 |
| 95% | 1.960 |
| 97% | 2.170 |
| 99% | 2.576 |
Por lo tanto, de forma general podemos decir que la media que hemos medido en la muestra (\( m \)) cumple lo siguiente:
La expresión anterior se lee así: la probabilidad de que la media \( m \) observada en la muestra esté entre el intervalo definido por la media de la población \( \mu \) menos el margen de error \( Z_{NC} \cdot \sigma / \sqrt{n} \) y la media de la población más el margen de error \( Z_{NC} \cdot \sigma / \sqrt{n} \) , es \( NC \) .
Como lo que nosotros queremos estimar es justamente la media de la población \( \mu \), podemos transformar la expresión anterior como sigue, cambiando de orden los elementos de la desigualdad:
Para comprender mejor esta expresión, retomemos el ejemplo anterior acerca de la población brasileña. Supón que obtenemos una muestra de n=500 personas, calculamos la media de minutos de TV vistos por esas 500 personas y resulta 415. Y supongamos por el momento que sabemos que la desviación típica en la población no supera los 100 minutos. Podríamos decir
Gracias al teorema central del límite podemos decir que en un 90% de los casos, la media de consumo de TV de la población brasileña está entre 407.6 y 422.4 minutos. En lugar de dar una estimación puntual (415) estamos dando una estimación, un margen de error (±7.4) y el nivel de confianza que tenemos en que la realidad esté dentro del margen de error (90%).
¿Y cómo me ayuda esto a decidir el tamaño de la muestra?
Muy fácil, solo tienes que decidir de antemano cuál es el error máximo que estás dispuesto a aceptar (\( e \) ) y el nivel de confianza que quieres tener en que ese error no va a ser superado (\( NC \) ).
Sabiendo que el error máximo es
solo tenemos que darle la vuelta a esta expresión
Volviendo a nuestro ejemplo. Imagina que no hemos hecho la encuesta aún, pero queremos tener un nivel de confianza del 90% de que la media que observemos en la muestra no se desvíe de la realidad en más de ±5 minutos. La muestra que necesitamos será de
Hemos redondeado al alza (1,082.4->1,083) porque queremos garantizar que no superamos el error de 5 minutos, pero es un detalle sin mucha importancia. Observa que la muestra resultante es mayor a la anterior de 500 individuos, porque el error máximo que pedimos (5) es más pequeño que el que teníamos antes (7.4).
¿Y si lo que quiero estimar es una proporción?
Supongamos que en lugar de estimar una media (minutos de TV) quiero estimar una proporción (porcentaje de fumadores). En este caso el problema es más sencillo, podemos simplificar las fórmulas anteriores de forma muy conveniente.
Llamemos \( p \) al porcentaje de fumadores en el total de la población brasileña. En este caso, la población se distribuye siguiendo una distribución de Bernoulli: una proporción \( p \) de la población fuma (fumar=1) y una proporción \( 1-p \) no fuma (fumar=0). Esta distribución es extremadamente simple y tiene una desviación típica \( \sigma = \sqrt{p(1 - p)} \). Por lo tanto, el tamaño de la muestra que garantiza un error máximo \( e \) es
Podemos simplificar un poco más esta expresión. Antes de hacer la encuesta no sabemos qué proporción de fumadores vamos a encontrar (para eso hacemos la encuesta). Pero sí podemos ponernos en el peor caso. Observa que la cantidad \( p(1 - p) \) resulta 0 tanto si \( p=0 \) como si \( p=1 \) . Es decir, si todo el mundo fuma o no fuma, la muestra que necesitamos es prácticamente nula. El peor caso se produce cuando la población es lo más diversa posible (\( p=0.5 \) ), es decir, cuando la mitad de la gente fuma.
Si uso este escenario pesimista, resulta
A diferencia del caso en el que estimábamos minutos de TV vistos, no necesitamos hacer ninguna hipótesis sobre la desviación típica de la población de origen, porque podemos usar el peor caso: la máxima desviación posible en una proporción.
¿Cómo se usa esta fórmula? Supón que queremos hacer una encuesta entre brasileños para estimar qué porcentaje de la población fuma y estamos dispuestos a aceptar un error máximo del 5% con un nivel de confianza del 90%. Resulta
Solo necesitamos encuestar a 271 personas. Importante: el error se define en términos absolutos. Es decir, si observamos un 40% de fumadores, tendremos un 90% de confianza de que la proporción real en la población esté entre 40%-5% y 40%+5% (no entre 40%×0.95 y 40%×1.05).
¿Y si la población no es infinita?
Se acostumbra a aceptar que una población con más de 100,000 individuos es infinita (algunos autores consideran 50,000 como el mínimo exigible). En general, en investigación de mercados las poblaciones objeto de estudio suelen cumplir este requisito. Pero en determinados casos podemos tener poblaciones pequeñas. Por ejemplo, una encuesta a empleados de una empresa.
En estos casos las fórmulas que hemos visto deben modificarse un poco. Te ayudamos a entender el porqué. Imagina un caso muy extremo en el que solo hay 10 personas en la población, la mitad fumadores y la otra mitad no fumadores. Y quieres una muestra de 2 personas.
Inicialmente, tienes un 50% de probabilidad de que el primer individuo de tu muestra sea fumador. Seleccionas un individuo y fuma. La probabilidad de que el segundo individuo sea fumador ya no es 50%, porque quedan solo 4 fumadores entre los 9 individuos no seleccionados. Ahora la probabilidad de que selecciones un fumador es 4/9=44%. La probabilidad de que fumen los individuos a seleccionar depende de los ya seleccionados.
Esta dificultad la puedes obviar cuando la población es de cientos de miles de individuos: el hecho de que los que vayas seleccionando fumen o no, apenas afecta a la probabilidad de los restantes. Pero con muestras finitas debes tenerlo en cuenta.
Relación entre error, nivel de confianza y tamaño de muestra
Recuerda que margen de error, nivel de confianza y tamaño de la muestra siempre van de la mano de allí la importancia de conocer el tamaño muestral a la perfección.. Modificar cualquiera de los 3 parámetros, altera los restantes:
1. Reducir el margen de error obliga a aumentar el tamaño de la muestra.
2. Aumentar el nivel de confianza obliga a aumentar el tamaño de la muestra.
3. Si aumenta el tamaño de mi muestra, puedo reducir el margen de error o incrementar el nivel de confianza.
¿Necesitamos hacer estos cálculos?
No, por eso disponemos de una calculadora que hace todo el trabajo por ti. Si estás tratando de estimar una proporción, sólo debes saber que el parámetro "nivel de heterogeneidad" es esta proporción esperada y que, en ausencia de información, deberás indicar un valor de 50%, como hemos hecho en este post.
Si lo que necesitas estimar es el tamaño de una muestra para calcular una media o hacer otro cálculo más complejo, te invitamos a que visites la sección de calculadoras avanzadas.
Esperamos haberos ayudado a interpretar el uso de nuestras calculadoras de muestras.
Respondiendo a una pregunta habitual de los lectores de este post: la primera persona que formuló el cálculo del tamaño de la muestra en estos términos fue William G. Cochran.
Te puede interesar: Cómo diseñar una investigación ad-hoc, Paneles de encuestas: Decisiones de mercado en 2024
Descubre nuestro servicio de muestras Ad-hoc: La solución perfecta para tus Necesidades de investigación
En Netquest, entendemos que cada proyecto de investigación es único y requiere una atención especializada. Por ello, estamos orgullosos de presentar nuestro servicio de Muestras Ad-hoc, diseñado para proporcionar soluciones de muestreo precisas y adaptadas a las necesidades específicas de tu estudio.
¿Por qué elegir nuestras Muestras Ad-hoc?
- Personalización Completa: Cada muestra se diseña a medida, asegurando que se ajuste perfectamente a los requisitos de tu investigación, desde estudios de mercado hasta análisis sociodemográficos detallados.
- Calidad y Fiabilidad: Nos apoyamos en nuestra avanzada plataforma tecnológica y en nuestra comunidad de respondientes comprometidos para garantizar datos de la más alta calidad.
- Experiencia y Soporte: Con años de experiencia en el sector, nuestro equipo de expertos te acompañará en cada paso, ofreciéndote el soporte necesario para que tu proyecto sea un éxito.
Al integrar nuestro servicio de Muestras Ad-hoc en tu proyecto de investigación, te beneficiarás de un proceso de muestreo que no solo cumple con tus expectativas, sino que las supera, permitiéndote obtener insights profundos y relevantes.







