No último post vimos como deve ser um bom desenho experimental Conjoint. Também vimos como calcular a eficiência, a medida que nos permite comparar desenhos. Nesse post veremos como construir um desenho que se ajuste aos nossos critérios (número de sets, alternativas por sets, etc.) e que seja eficiente.
E se deixarmos ao acaso?
Um bom desenho, na verdade, é um desenho totalmente aleatório. Queremos que todos os níveis apareçam de formas iguais e que todas as comparações de níveis se repitam algumas vezes. Devemos gerar desenhos de forma randômica, dando a mesma probabilidade de inclusão em todos os níveis. É o que chamamos de desenho randomizado.
Mas analisar as coisas através do acaso é muito arriscado. Se a amostra é muito grande e cheia de sets, não é bom contar com a sorte do acaso. A realidade é que o custo da amostra é caro e não se pode pagar milhares de amostras para todos os estudos. O mais apropriado é definir um desenho concreto e específico para o tamanho da amostra pré-determinada. Por isso é possível garantir que o projeto seja equilibrado. Essa estratégia é conhecida como desenho planejado.
Desenhos pré-definidos
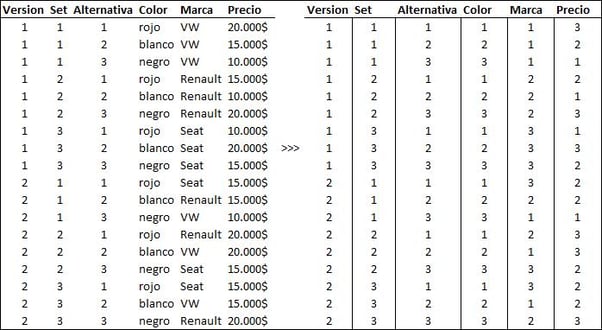
Dificilmente você será a primeira pessoa a sentir a necessidade de criar um desenho do zero. Provavelmente devem existir projetos pré-definidos que poderão ser utilizados como objeto de estudo. Para certas combinações de números e níveis de atributos, são desenhos ideais - perfeitamente equilibrados e ortogonais. São construídos utilizando um instrumento matemático chamado "matrizes ortogonais". Abaixo você verá algumas das combinações. O desenho é em formato de matriz. Cada linha é um produto mostrado e cada coluna é correspondente ao nível de atributo.
Desenho para 3 atributos, com 2 níveis por atributo (Geralmente se expressa como 2x2x2 ou 23)
1 1 1
2 1 2
1 2 2
2 2 1
Desenho para 2 atributos, um com 2 níveis e outro com 3 (2131)
1 1
1 2
1 3
2 1
2 2
2 3
Desenho para 7 atributos de 2 níveis (27)
1 1 1 1 1 1 1
2 1 2 1 2 1 2
1 2 2 1 1 2 2
2 2 1 1 2 2 1
1 1 1 2 2 2 2
2 1 2 2 1 2 1
1 2 2 2 2 1 1
2 2 1 2 1 1 2
Infelizmente, nem sempre vamos encontrar um desenho pré-estabelecido que se encaixa em nosso perfil. Precisamos buscar uma solução assertiva para gerar desenhos com o nosso problema de pesquisa.
Criação de desenhos personalizados
Para criar desenhos customizados é necessário usar um algoritmo de busca. É um algoritmo baseado na proposta de Warren F. Kuhfeld em 1994, inspirado pelo algoritmo de Fedorov.
Para ilustrar como é feito, seguem os principais pontos que analisamos para nossos clientes:
- Elaborar uma lista de candidatos, isso é, todas as combinações possíveis nos níveis de atributos que definimos.
- Ordenar a lista de forma aleatória.
- Criar um primeiro desenho baseado numa seleção aleatória dos produtos.
- Avaliar a eficiência-D do desenho aleatório inicial.
- Substituir o primeiro produto incluído no desenho pelos produtos da lista de candidatos.
- Avaliar se, para cada substituição, a eficiência-D melhora ou piora. Se a melhora, manter a mudança, se piora, rejeitamos.
- Repetir a operação (5) e (6) para todos os produtos de desenho.
- Após substituir todos os produtos do desenho, retornaremos ao início: substituiremos todos os produtos novamente. Pela metodologia do Conjoint, a criação do desenho do estudo se dá através de tentativa e erro. Assim, é necessário repetir algumas vezes para que tenhamos certeza que o desenho não esta enviesando.
- O algoritmo é analisado inúmeras vezes, recomeçando cada vez com um desenho diferente. Escolhemos o projeto com o melhor resultado e eficiência.
O algoritmo descrito é totalmente útil para projetos Conjoint reais, onde o número de atributos e a quantidade de níveis de cada atributo não se ajusta ao padrão pré-definido. A outra vantagem é a possibilidade de incluir ao algoritmo as restrições do desenho.
Restrições do desenho
Um Conjoint permite estudar diferentes tipos de produtos: automóveis, seguros, cartões de crédito, contratos de telefonia, etc. Cada tipo de produto tem suas próprias características. Os atributos e a maneira como se combinam para criar produtos variam muito de um setor para outro. As vezes, o gerente de produto por trás de um estudo Conjoint quer impor certas restrições sobre os produtos que irá mostrar na pesquisa.
Uma restrição muito comum é definir produtos proibidos, combinações de atributos que nunca devem ser exibidos. Por exemplo, em um estudo Conjoint sobre carros, pode ser que uma das marcas estudadas não ofereça alguma cor específica ou não tenha carros com motores a diesel. Se você criar um algoritmo padrão, essas combinações certamente apareceriam.

Outra restrição comum é definir comparações proibidas, produtos que não devem aparecer dentro de um set. Por exemplo, podemos evitar a comparações produtos dominantes. Diz-se que um produto domina outra quando o primeiro é objetivamente melhor que o outro. Imaginem um carro em nosso estudo. Dois produtos idênticos em todos os atributos (mesma marca, mesmo potência, mesma cor), mas um é bem mais barato que o outro. Qualquer entrevistado racional seleciona o produto de menor preço. Incluir esta questão no estudo não produziria nenhum problema mas não nos forneceria nenhuma informação relevante.
Algoritmos personalizados
A boa notícia é que o algoritmo descrito acima pode ser personalizado. Por exemplo, o caso dos produtos proibidos é resolvido através da sua remoção da lista dos candidatos. As combinações proibidas podem ser controladas através da adição de um passo no algoritmo, de maneira que antes de adicionar ou rejeitar um produto no desenho, é necessário verificar se o mesmo pode conviver com os que já estão no set de destino.
A má notícia é que, as vezes, as regras que definem os produtos e comparações proibidas não são simples. É possível surgir restrições, por isso precisamos de um programador para reformular os algoritmos de busca e os desenhos. Realizar personificações em excesso diminui a eficiência do desenho. O mais recomendado é restringir o menos possível.
Se uma combinação de atributos não existe no mercado, isso não significa que não podemos incluí-la no experimento. Se estamos tentando medir como os consumidores valorizam cada atributo, estas combinações inexistentes pode nos dar muita informação importante. Por exemplo, apesar de não oferecer veículos da cor vermelha, a marca poderá descobrir novas oportunidades de gerar mais clientes.
Esta foi a última cápsula extensa sobre a explicação de como projetar experimentos Conjoint. Na próxima cápsula iremos abordar como programar o questionário Conjoint e passar pela um aspecto fundamental nesses estudos: a análise.