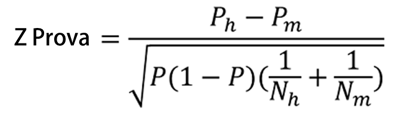Anteriormente explicamos nesse post como definir o tamanho de uma amostra e garantir que os dados obtidos estejam dentro de uma margem de erro controlada. Nesse post vamos investigar sobre problemas relacionados às diferenças sobre os dados de uma pesquisa. Vamos analisar se essa diferença é estatisticamente significativa.
Isso é real ou é devido ao acaso?
Esta é uma pergunta que nos fazemos diversas vezes, inclusive em situações da vida cotidiana. Vamos analisar a seguinte situação: Você costumar ir para o trabalho de carro através da rota A e leva 25 minutos em média. Durante um mês, decidiu tentar uma nova rota B, onde demorava 23 minutos. Realmente a rota B é mais rápida que a rota A? Ou essa diferença de 2 minutos é devido ao acaso? Por exemplo, e se durante esse mês o o trânsito estava mais fluído? Se a diferença não é devida ao acaso, dizemos que é uma diferença estatisticamente significativa.
São inúmeras as situações em que precisamos ter certeza de que as diferenças que observamos não são explicadas por acaso. É a base do método científico. Por exemplo, vamos pensar sobre uma pesquisa médica. Temos um novo medicamento que necessitam verificar se o produto provoca o efeito desejado. Neste caso, administramos uma amostra da população que utilizou o medicamento e comparamos os resultados com uma amostra de pessoas que utilizaram um medicamento "placebo", ou seja, um medicamento que não tem nada em sua fórmula. Quando obtivermos os resultados, precisamos ter certeza absoluta que o efeito de cura é real. Esse tipo de prova são as mesmas que normalmente realizam-se com medicamentos homeopáticos. É por isso que a comunidade médica não aceita esse tipo de medicamento como eficaz.
Com o surgimento da internet, esta metodologia se tornou mais popular do que nunca. Os testes A/B são utilizados com muita frequência no desenvolvimento de páginas web. Por exemplo, em um site de e-commerce, 5% dos visitantes acabam comprando um produto (versão A do site). Queremos testar se o tamanho das imagens dos produtos influencia no aumento das vendas. Vamos fazer um teste A/B, analisando aleatoriamente 2 versões do site, versão A com o tamanho normal dos produtos e a versão B, com os produtos em tamanho maior. Vamos medir a navegação dos usuários e as conversões. Notamos que a versão B do site vendeu uma média de 5,5%. Como podemos ter certeza que a diferença de 0,5% é devido ao tamanho maior dos produtos?
As estatísticas serão muito úteis para as perguntas. Vamos fazer um teste de hipóteses e ver como ele funciona.
Teste de Hipóteses
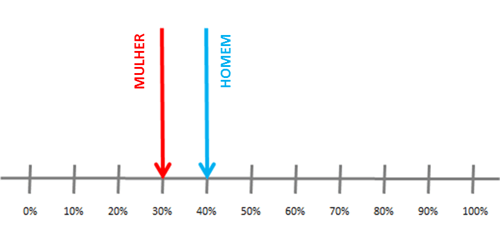
Vamos ilustrar para que a aprendizagem seja mais intuitiva. Vamos supor que precisamos fazer uma pesquisa a 100 homens e 100 mulheres, perguntando se eles praticam esporte. Ao analisar as respostas, observou-se que 40% dos homens praticam esporte em comparação com 30% das mulheres. Segue a representação desses dados no gráfico abaixo:
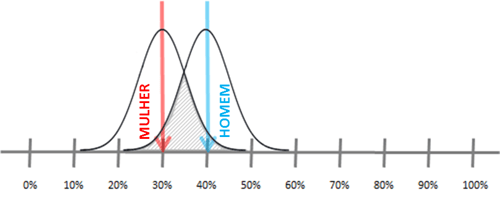
Vimos neste post que, se calcularmos uma estatística através de uma amostra no lugar do universo total, nossos dados estarão sujeitos a uma grande margem de erro. Quanto menor for a amostra utilizada, maior é a margem de erro. Por isso, a maneira mais correta de representar os resultados desta pesquisa seria através deste gráfico:
No gráfico acima representamos a incerteza que temos sobre os percentuais de homens e mulheres que praticam esportes. Quando usamos este olhar, vemos que a margem de erro de ambos os dados (homens e mulheres) se sobrepõe consideravelmente, ou seja, é relativamente fácil ver que essa diferença entre homens e mulheres não é real, é um efeito de erro de amostragem quando trabalhamos com uma amostra pequena. Esta marca em cinza representa esse risco: a probabilidade da diferença devido ao erro, por isso não notamos nenhuma diferença significativa.
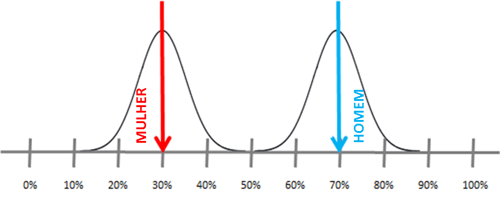
Como podemos ter certeza que a diferença é realmente significativa? O ideal é que a diferença entre os dados de homens e mulheres seja grande, onde a margem de erro fique evidente, de acordo como vemos no gráfico abaixo:
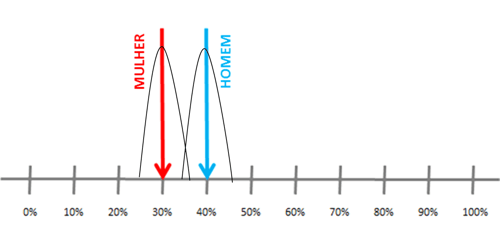
Para obter uma garantia maior sobre a diferença significativa, é necessário trabalhar com amostras de tamanho maior. Ou seja, precisamos trabalhar com uma amostra maior, gerando uma margem de erro menor que permita detectar diferenças significativas, de acordo com o gráfico a seguir:
Podemos medir isso de maneira objetiva?
Sim, geralmente é realizado um teste de hipótese (Prova objetiva sobre a causa das diferenças). Primeiro, definimos as seguintes quantidades:
- Nh = tamanho da amostra de homens
- Nm = tamanho da amostra de mulheres
- Xh = número de homens que praticam esportes
- Xm = número de mulheres que praticam esporte
A partir dessa quantidade, em primeiro lugar, calcularemos a proporção global de pessoas que praticam esportes, sejam eles homens ou mulheres:
- P = (Xh+Xm)/(Nh+Nm)
Também podemos calcular a proporção de atletas entre os homens e entre as mulheres, que são dados diferentes e queremos verificar:
- Ph = Xh/Nh
- Pm = Xm/Nm
Em seguida, propomos dois cenários possíveis:
- H0 (hipótese nula) = Não há diferenças entre as amostras, a diferença observada é devida ao acaso.
- H1 (hipótese alternativs) = A diferença é estatisticamente significativa, ambas as amostras são realmente diferentes em relação à variável estudada.
Para aceitar a hipótese alternativa, precisamos que a diferença entre as duas medidas de proporções (Ph e Pm) seja o suficiente para ter uma % de confiança alta, onde essa diferença não seja um erro amostral, sendo apenas um erro de distribuição normal ou Gaussiano. Para isso, vamos calcular o seguinte:
É importante verificar que Z não deverá exceder a quantidade é dada pelo nível de confiança que desejamos. É muito comum trabalharmos com um intervalo de confiança de 95%, o que corresponde a um valor de Z = 1,96. Portanto:
- Se Zprova <1,96 Aceitaremos que não há diferenças significativas entre homens e mulheres, com um nível de confiança de 95%.
- Caso contrário, Aceitaremos que há diferença observada entre homens e mulheres é significativa, com um nível de confiança de 95%.
Voltando ao exemplo...
Podemos fazer esses cálculos utilizando nosso exemplo inicial. Lembre-se: 100 homens e 100 mulheres, 40 homens e 30 mulheres esportistas. Temos:
- Nh = 100
- Nm = 100
- Xh= 40
- Xm= 30
Estes dados resultam em Z = 1,48, que se for inferior a 1,96 não nos permitem afirmar que a diferença é significativa. Se, no entanto, esse resultado foi obtido com uma amostra de 200 homens e 200 mulheres, o Z resultante seria 2,10, o que nos permitiria aceitar a hipótese.
Considerações finais
É muito importante considerar o tamanho da amostra. Em alguns casos, com amostras extremamente pequenas, grandes diferenças são observadas e mesmo assim não são estatisticamente significativas. Isso não significa que esta diferença não seja real, simplesmente significa que não podemos ter uma garantia suficiente.
Por outro lado, com amostrar muito grandes, podemos encontrar pequenas diferenças significativas, o que na prática não será muito informativa.