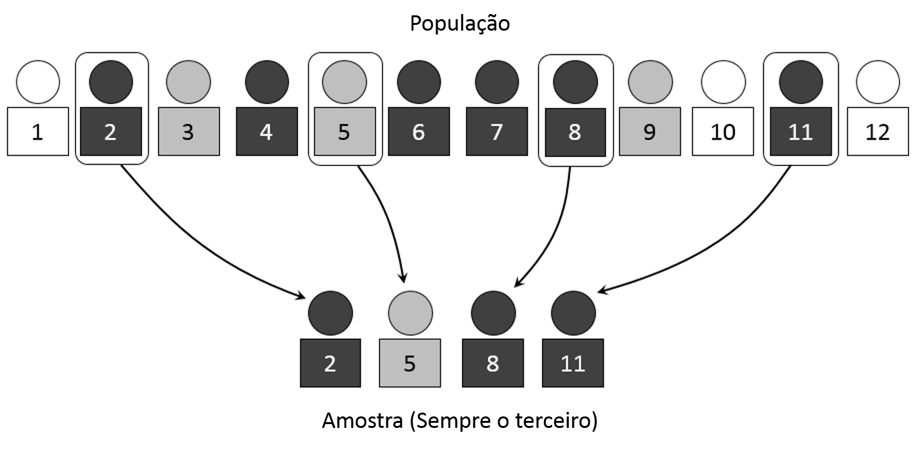
Continuando com a nossa série de posts dedicados as técnicas de amostragem, iremos examinar hoje um tipo de amostragem estratificada conhecida como amostra sistemática.
Anteriormente, quando a informática não estava tão desenvolvida, a amostra sistemática era muito popular. Antigamente existia inúmeros problemas que quebravam a cabeça dos pesquisadores: selecionar de forma aleatória dentro de uma amostra. A medida que os computadores facilitaram esta tarefa de gerar números aleatórios, essa dificuldade desapareceu.
Esta técnica continua sendo utilizada para selecionar indivíduos a longo prazo. Por exemplo, para estudar a satisfação de um serviço, podemos eleger sistematicamente e perguntar a 1 de cada N clientes que nos visitam. Nessas circunstancias onde pode existir diferentes variáveis entre os indivíduos em diferentes períodos de tempo, a amostra sistemática pode ser mais precisa que a amostra aleatória pura.
Em que consiste a amostra sistemática?
É uma técnica dentro da categoria de amostragem probabilística – que requer certo controle do marco amostral entre os indivíduos selecionados junto com a probabilidade que sejam selecionados – consiste em escolher um indivíduo inicialmente de forma aleatória entre a população e, posteriormente, selecionar para amostra cada enésimo indivíduo disponível no marco amostral.
A amostra sistemática é um processo muito simples e que só requer a seleção de um indivíduo aleatório. O restante é um processo rápido e simples. Os resultados obtidos são representativos da população, de forma similar a amostra aleatória simples, sempre quando não exista nenhum fator intrínseco na forma que os indivíduos estão listados e que se reproduzam certas características populacionais em cada número especifico de indivíduos. Esse sucesso realmente é pouco frequente.
O processo
De forma concreta, o processo que seguiríamos numa amostra sistemática seria:
1- Elaborar uma lista ordenada dos N indivíduos da população (marco amostral).
2- Dividir o marco amostral em N fragmentos, onde N é o tamanho da amostra que desejamos. O tamanho desses fragmentos será:
K=N/n
3- Número de inicio: obtemos um número aleatório inteiro A, menor ou igual ao intervalo. Este número corresponderá ao primeiro sujeito que iremos selecionar para a amostra dentro do primeiro fragmento que dividimos a população.
4- Seleção dos N-1 indivíduos restantes: Selecionamos os seguintes indivíduos a partir do indivíduo elegido aleatoriamente, mediante uma sucessão aritmética, selecionando aos indivíduos do resto do fragmento que dividimos a amostra, onde está o sujeito inicial. Selecionaremos os indivíduos:
A, A + K, A + 2K, A + 3K, ...., A + (n-1)K
Exemplo
Suponhamos um marco amostral de 5.000 indivíduos e desejamos obter uma amostra com 100 deles. Em primeiro lugar, dividimos o marco amostral em 100 fragmentos de 50 indivíduos. Selecionamos um número aleatório entre 1 e 50 para extrair o primeiro indivíduo de forma aleatória: por exemplo o número 24. A partir deste indivíduo, está definida como será extraída a amostra, com intervalos de 50 unidades, conforme a equação: 24, 74, 124, 174, …, 4.974
Propriedades da amostra sistemática
As principais vantagens são:
- Obtém boas propriedades de representatividade, similar a amostragem aleatória simples, porém de forma mais rápida e simples, evitando a necessidade de gerar tantos números aleatórios como indivíduos na amostra.
- Pode garantir uma seleção perfeitamente equivalente a população. Isto pode ser uma utilidade se os grupos dentro dos universos se distinguem, evitando a necessidade de usar camadas/estratos. Se existe diferentes variáveis entre os indivíduos dos fragmentos, essa amostra pode ser melhor que a aleatória. Logo vamos demonstrar.
Como desvantagem, só existe a possibilidade que a ordem dos candidatos listados na amostra tenha algum tipo de periodicidade oculta que coincida com o intervalo escolhido para gerar a amostra sistemática. Neste caso, podemos gerar uma amostra duvidosa.
Eficiência da amostra sistemática
A amostra sistemática foi idealizada para aperfeiçoar as propriedades da amostra aleatória simples, porém o grau melhora de acordo com as propriedades do universo estudado.
Para entender as propriedades de amostragem, devemos:
Se prestamos atenção no intervalo ou coeficiente de elevação de acordo com o tamanho da amostra que necessitamos, só há um elemento aleatório dentro do processo de amostragem: a unidade inicial que selecionamos do primeiro bloco de indivíduos. O resto continua fixo. Quer dizer que: só temos K possibilidades de obter amostras diferentes, e para obter a amostra é só escolher K de amostras disponíveis.
É possível demonstrar que quanto maior a variação dentro das K possibilidades de amostras, mais precisão ganhamos usando a amostragem sistemática em relação a amostragem simples.
A amostra sistemática é mais precisa que a aleatória simples quando a variabilidade dentro das possíveis amostras é superior a variabilidade dentro das unidades da população. A precisão da amostra sistemática coincide com a aleatória simples quando ambas variabilidades coincidem, ou seja, quando os elementos da população são totalmente aleatórios.
ÍNDICE: Série "Amostragem"
- Amostragem: O que é e por quê funciona
- Amostragem probabilística e não probabilística
- Amostragem probabilística: Amostar aleatória simples
- Amostragem probabilística: Amostra estratificada
- Amostragem probabilística: Amostra sistemática
- Amostragem probabilística: Amostra por conglomerados
- Amostragem não probabilística: Amostra por conveniência
- Amostragem não probabilística: Amostra por quotas
- Amostragem não probabilística: Amostra por bola de neve