Cápsula VIII : Análise agregada de um Conjoint

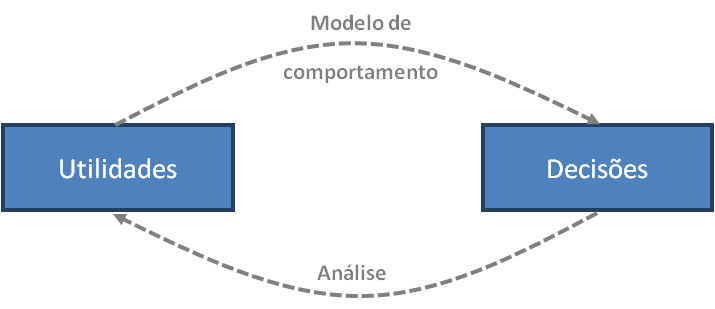
Podemos analisar um Conjoint de diversas maneiras. Cada uma é baseada em um modelo comportamental: uma forma matemática que descreve o processo de decisão das pessoas. O mais simples é o modelo de Regressão Logística Multinomial.

Como se analisa um Conjoint

A análise Conjoint deve sempre seguir este processo:

1. Definimos um modelo de comportamento que relaciona com as utilidades dos produtos com as decisões dos indivíduos. Este modelo permite prever a partir das utilidades, a probabilidade de que um indivíduo tem de escolher um produto entre vários disponíveis.
2. A análise consiste em fazer o caminho inverso. Exibindo as decisões dos indivíduos em relação a produtos, buscamos os argumentos que explicam melhor as decisões que temos observado.

O  modelo de Regressão Logística multinomial (MNL)

Neste post veremos o modelo mais simples usado para análise Conjoint, o modelo de Regressão Logística multinomial (MNL – MultiNomial Logistic). Este modelo aceita alternativas bastante restritas, porém sua análise é uma tarefa muito simples. O modelo foi desenvolvido na década de 70, numa época em que os computadores não tinham capacidade de cálculo avançado. Ter um modelo simples foi uma vantagem crucial.

Hipóteses do Modelo MNL

Todo o modelo comportamental assume uma hipótese sobre os respondentes e como eles se comportam. O modelo MNL é baseado nas suposições:

• O erro nas estimativas de utilidade tem uma probabilidade muito pequena: Esta distribuição é semelhante ao normal - a probabilidade é alta em um valor central e diminui rapidamente à medida que os afastamos - mas se descreve por uma função integrada. Esta suposição simplifica as expressões matemáticas do modelo.
• Parte da utilidade que não observamos não está relacionada com os atributos: É uma hipóteses técnica e importante. No modelo MNL assumimos que existem alguns fatores que não estamos considerando e que fazem com que as estimativas não sejam perfeitas. Os fatores não observados são a fonte do erro de estimativa, ou seja, temos que considerá-los para não afetar os atributos analisados porém precisam ser independentes.
• Independência das alternativas irrelevantes (IAI). Sobre a hipótese acima, o modelo MNL nos diz que a probabilidade relativa de escolher uma opção A sobre outra B não muda interfere na presença ou ausência de outras opções, são independentes. A hipótese de IAI é a base de muitos modelos de decisão, mas tem sido questionada por vários psicólogos que mostram que os seres humanos nem sempre se decidem assim.

Um exemplo: O famoso problema do ônibus azul - ônibus vermelho. Um viajante tem a opção de ir para o trabalho de carro ou no ônibus azul. Suponhamos que a utilidade dos dois meios de transporte sejam iguais, de modo que as probabilidades de escolha são iguais: = Pbus_azul Pcarro = 1/2. Neste caso, a relação de probabilidade é uma só: P_carro/P_{bus_azul}=1.

Agora imagine que uma nova opção de transporte é introduzida, o viajante descobre que o ônibus vermelho é exatamente igual ao ônibus azul. A probabilidade de que o viajante tem de escolher o azul é igual ao vermelho, de modo que a razão entre as suas probabilidades é um: P_carro/P_{bus_azul}=1. No entanto, o modelo MNL exige que a relação  P_carro/P_{bus_azul}  continua a ser a mesma (1), tendo uma nova alternativa ou não. As únicas probabilidades de escolha que respeitam as duas condições são: P_carro=P_{bus_azul}=P_{bus_vermelho}=1/3, que é precisamente a probabilidade que o modelo MNL prevê.

Não parece uma boa previsão ... No mundo real, era de se esperar que a probabilidade de que o viajante tem de escolher o carro seja igual ao eleger um novo ônibus, pois a nova opção era igual a opção já existente. Ou seja, seria de esperar a equação : P_carro=1/2 y P_{bus_azul}=P_{bus_vermelho}=1/4. Em um caso assim, o modelo MNL não é o mais indicado.

• Todos os indivíduos percebem o mesmo valor de um atributo. O modelo MNL não admite variação aleatória de preferências entre os indivíduos. O que isto significa? Significa que duas pessoas idênticas podem ter diferentes preferências. Qualquer diferença deve vir explicado por um fator objetivo, estando ou não no modelo.

Mas se todos os mesmos indivíduos recebem atributos de utilidade iguais, como você explica o modelo que nem todos respondem o mesmo questionário Conjoint? Para o modelo MNL, as diferenças em suas respostas se devem aos fatores que não estamos observando e que geram erro de estimativa.

Esta hipótese pode parecer muito limitante, mas não é assim. Na prática, você pode ver a questão de uma forma mais simples: as estimativas do modelo MNL para cada atributo a média da população. É por isso que nos referimos a um modelo de análise agregada, não individual.

Probabilidade de escolha MNL

Suponhamos que um indivíduo tem de escolher entre quatro diferentes produtos. Vamos imaginar que conhecemos a utilidade desses quatro itens: U1, U2, U3 e U4. O modelo MNL prevê uma probabilidade de que o decisor escolha a primeira opção de:

P₁ = e^U1 /( e^U1+ e^U2+ e^U3+ e^U4)

Para outras opções, as chances seriam equivalentes. Como você pode ver, é uma expressão simples, nós temos que exponencial as utilidades ("e" é operador exponencial do Excel). Esta fórmula é muito simples porque consideramos que o erro de estimativa segue um tipo de distribuição de valores extremos.

Segue um exemplo. Imagine que estimamos a utilidade de dois atributos com dois níveis em estudo Conjoint sobre carros:

Atributo 1 = Cor.

• Branco -> U_branco=-0,5
• Preto-> U_preto=0,2

Atributo 2 = Marca.

• VW -> U_vw=1,2
• Renault-> U_renault=0,8

Se quisermos prever a probabilidade de um comprador escolher um dos quatro possíveis carros que resultam desses atributos (supondo que você foi forçado a comprar uma das 4 opções), devemos fazer a seguinte operação:

1. Calcular os atributos das diversas opções com a soma das utilidades dos atributos que os compõem.

Carro 1, VW Branco à U1 = U_vw + U_branco =1,2-0,5=0,7

Carro 2, VW Preto à U1 = U_vw + U_preto =1,2+0,2=1,4

Carro 3, Renault Branco à U1 = U_renault + U_branco =0,8-0,5=0,3

Carro 4, Renault Preto à U1 = U_renault + U_preto =0,8+0,2=1,0

2. Avaliar a probabilidade das opções

P_carro1= e^U1 /( e^U1+ e^U2+ e^U3+ e^U4)= e^0,7 /( e^0,7+ e^1,4+ e^0,3+ e^1,0)=20%

P_carro2= e^1,4 /( e^0,7+ e^1,4+ e^0,3+ e^1,0)=40%

P_carro3= e^0,3 /( e^0,7+ e^1,4+ e^0,3+ e^1,0)=13%

P_carro4= e^1,0 /( e^0,7+ e^1,4+ e^0,3+ e^1,0)=27%

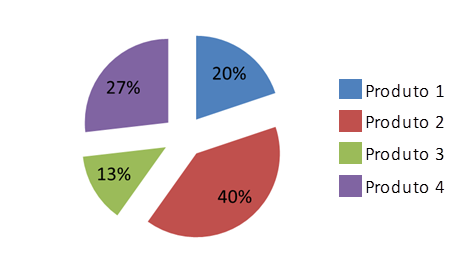Nós temos uma fórmula que nos permite prever a proporção de que um produto seja escolhido a partir da sua utilidade e de seus concorrentes. Ou seja, o market share entre os compradores.

 E a análise? Como é feita?

Já aprendemos passar de utilidade para probabilidade. Mas o que queremos fazer é o oposto. As respostas dos participantes são eleições (decisões) frente a uma oferta de dois ou mais produtos. Se você perguntasse a 100 pessoas que selecionem entre a opção A e opção B, e 20 optam pela A, compreendemos que 20% da população prefere A do que B.

Pois bem, essa % de pessoas que optaram por A é equivalente a probabilidade de seleção de A sobre B. Com isso, a tarefa de análise será buscar as utilidades de A e B e prever a probabilidade entre a escolha de A versus B.

Parece fácil mas não é. A e B são produtos compostos por vários atributos e a utilidade são os fatores que precisamos encontrar. Essas competências são combinadas de diferentes maneiras para formar produtos C, D, E, etc. cuja as probabilidades de seleção estimamos pelo Conjoint. No final, os dados da pesquisa nos dará muitas opções em relação à múltiplas combinações de atributos.

Como podemos encontrar competências que se encaixam com todas as escolhas dos entrevistados de uma só vez?

A resposta é que não podemos fazê-lo. Conseguimos estimar as competências e minimizar o máximo os erros para bons resultados. Para fazer isso, costuma-se usar o seguinte método:

1. Partimos das utilidades iguais para todos os atributos.
2. Calculamos as probabilidades de escolha para cada pergunta do questionário.
3. Calculamos os erros entre as previsão de resposta e as respostas da pesquisa.
4. Modificamos as utilidades para reduzir a probabilidade de erros.
5. Repetimos os passos 2-4 até chegarmos em bons resultados com erros insignificantes.

A análise MNL é uma maneira simples de analisar um Conjoint, mas só nos permitem tirar conclusões a nível agregado. Podemos falar sobre as preferências da amostra, mas não as preferências de um indivíduo ou grupo de indivíduos em particular. No próximo post, vamos ver um método mais sofisticado que terá muita utilidade.