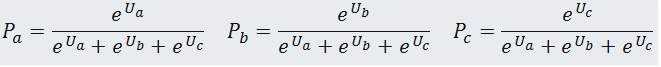Depois de nossa introdução aos estudos Conjoint, continuaremos nossa serie de posts dedicada a esta metodologia falando do conceito de utilidade, um conceito abstrato, mas de enorme utilidade para descrever o comportamento do consumidor.
Qual é a utilidade?
No post anterior vimos que um estudo Conjoint é capaz de calcular alguns números que representam a utilidade que é atribuída por nossos consumidores a cada um dos atributos de um produto. Mas, o que utilidade e como devemos interpretá-la?
A utilidade é um termo usado em economia para descrever o valor que recebe um consumidor de um bem (um produto um serviço, uma decisão qualquer...). A utilidade pode medir o quanto alguém aprecia um filme, ou a sensação de segurança que obtém ao comprar um cadeado. É possível considerar a utilidade de qualquer objeto ou circunstância, desde comer uma maça até votar em um candidato na eleição. Qualquer decisão que um indivíduo faz em sua vida diária vemos como uma comparação entre a utilidade que lhe proporciona essa decisão frente a outra. Ou frente a não tomar uma decisão. Por fim, o indivíduo escolhe as opções que proporcionaram maior utilidade.
Só as diferenças em utilidade importam
Podemos ir um pouco mais além e quantificar numericamente a utilidade, de maneira que não só poderemos dizer que uma decisão é mais útil que a outra, se não quanto mais útil é. Isso é justamente o que faz uma análise Conjoint. Estes números usados para medir utilidades só são validos para fazer comparações.
Vejamos alguns exemplos que ilustram este principio. Afirmar que a utilidade que me proporciona o produto A é 100 não me dá nenhuma informação. Não significa nada em si mesmo. Utilidade =100 não tem sentido ao ser considerado de forma isolada.
Se a utilidade que me proporciona o produto A é 100 e a do produto B é 12.000, as utilidades começam a ter sentido. A comparação de ambas as quantidades me informa que B é mais útil para mim do que A, e que, portanto vou escolher B. Entretanto, não poderia afirmar que B me proporciona 120 vezes mais utilidade que A, porque a utilidade não é uma quantidade.
Do mesmo modo, o sinal da utilidade pode ser positivo ou negativo, isso não afeta sua interpretação. Se uma opção A tem uma utilidade de -15 e uma opção B de -10, selecionarei a segunda por ser maior que a primeira. A maior preferencia que terei por B é mais idêntica a que teria se as utilidades fossem 0 e 5 respectivamente: há uma diferença de 5 na utilidade em ambos casos.
A utilidade: racional, mas subjetiva
Na economia assumimos que o individuo se comporta de forma racional, e que por isso sempre maximiza a utilidade em suas decisões. Cada vez que um indivíduo escolhe, atua racionalmente se escolher a opção de maior utilidade.
Entretanto, a utilidade não é um conceito objetivo, mas que se define direto a um individuo, tendo em conta todas as circunstâncias que o rodeiam. A decisão de comer um chocolatinho pode ser prejudicial à saúde de uma pessoa, inconveniente se o comparamos com comer uma fruta. Mas, se o indivíduo, no momento de tomar sua decisão, ignora este dano ou simplesmente prioriza o disfrute que o chocolate vai proporciona-lhe neste momento, estará percebendo maior utilidade do chocolatinho que o da fruta. O cálculo de utilidade tem em conta todos os fatores que conduzem a certa decisão.
Relação entre utilidade e escolha
Um indivíduo sempre escolhe a opção que mais utilidade lhe proporciona. Se A tem utilidade de 100 e B de 120, escolherá B. E se A tem uma utilidade de 100 e B de 101, seguirá escolhendo B. Então, qual importância tem a diferença de utilidade? Por acaso só importa o fato de que uma opção tem maior ou menos utilidade que outra?
Estritamente é certo: uma vez que conhecemos a utilidade que percebe uma pessoa das diferentes opções, só importa qual é a de maior utilidade. O indivíduo sempre escolherá essa opção, não importa se perto ou longe que estejam as utilidades do restante das opções.
O problema é que não podemos conhecer a ciência certa da utilidade que percebe uma pessoa. Só podemos tratar de medir através de diferentes métodos. O Conjoint é um desses métodos.
Por que é importante a distinção entre conhecer a utilidade e medi-la? Porque toda medição carrega um erro. Suponhamos que meço utilidades através de um Conjoint, perguntando a um individuo sobre suas preferências a respeito de várias comparações de produtos. Se o indivíduo se equivoca ao responder uma pergunta estará introduzindo um erro em minha medida de sua utilidade. Assim mesmo, se quando lhe descrevo os produtos e não foi incluído os atributos que realmente afetam sua decisão, pode ser que sua resposta e fatores não observados - introduzam certo erro de medida na utilidade.
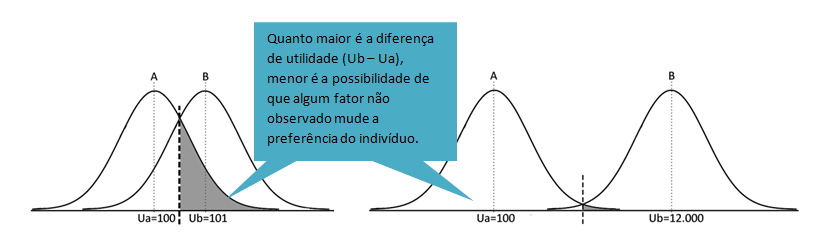
Estes erros de medida faz com que as diferenças de utilidades sejam mais relevantes. Se a utilidade que medimos de A é 100 e a B é 101, pode ser que os erros de medida estejam desviando minha medição o suficiente para que na realidade a utilidade de B seja 99. Se isso passar, minhas medições estariam me dizendo que o indivíduo escolherá B, mas na realidade será A. No entanto, se a medida de A é 100 e a de B é 12.000, é muito mais difícil que os erros possam fazer que na realidade a utilidade de B esteja por baixo de A. Minha previsão da escolha do individuo é muito mais robusta.
Probabilidades de escolha
Assim chegamos a um conceito chave, o conceito de probabilidade de escolha: é a probabilidade de que um indivíduo tome uma decisão concreta, tendo em conta a utilidade que usou para medir cada opção e a possibilidade de que o erro devido a fatores não observados mude essas utilidades.
Se determinarmos que a opção A e a opção B tem idêntica utilidade, diremos que a probabilidade de escolha tanto de A como de é de 50%. Se a utilidade de A é 10 e a utilidade de B é 11, diremos que a opção B tem uma probabilidade de escolha maior que A., mas só ligeiramente, porque um pequeno erro de medição poderia fazer com que A superasse a B. Assim, se a utilidade de A é 10 e B é 12.000, a probabilidade de escolha de B se aproximará ao 100%.
Só nos resta resolver uma questão. Com determinamos a relação entre utilidade e probabilidade de eleição? O que determina a diferença de utilidade de 1 é grande ou pequena?
Modelo de comportamento
A reposta nos facilita o modelo de comportamento. É o modelo estatístico que determina a relação entre as utilidades e as decisões dos consumidores (é dizer, as probabilidades de eleição). O veremos com maior detalhe nos próximos posts, mas aqui damos uma visão geral desta questão.
Existem diferentes modelos de comportamento. Alguns são mais simples e outros mais complexos. Teremos que escolher o melhor modelo para o problema que esteja estudando (e para as capacidades de analises que tenho).
Vejamos um exemplo. O modelo de comportamento mais amplamente usado em estudos Conjoint é o Logit Multinomial (MNL ). Este modelo é muito popular por sua simplicidade, graças a algumas hipóteses que nem sempre vamos poder assumir. A principal é assumir que a utilidade é a mesma para todo mundo e que se os indivíduos elegem diferentes, deve-se a atributos não observados, que podem ser diferentes para diferentes pessoas, e que geram erro de medição. Segundo este modelo, se observássemos todos os atributos dos produtos, esse erro seria nulo e poderíamos predizer perfeitamente as decisões das pessoas.
Sabemos que na pratica não és possível observar todos os fatores, por tanto sempre teremos erro devido a fatores não observados. MNL modela este erro mediante uma distribuição de probabilidade conhecida como distribuição de valor extremo (extreme value) . É uma distribuição parecida com a normal ou gaussiana: tem maior densidade em sua zona central (o valor 0 é o mais provável) e um rápido decaimento a medida que nos distanciamos do valor central. Mas a diferença da distribuição normal, a distribuição tipo valor extremo é integral e nos permite conseguir uma simples formula que relaciona utilidades e probabilidades de escolha.
Para um caso com três opções (A,B e C) para as que estimamos que a utilidade de cada opção é Ua, Ub e Uc, a probabilidade de que um individuo escolha cada uma das opções é:
É possível estender esta formula para qualquer número de opções. E poderá comprovar facilmente que a fórmula tem propriedades muito boas.
- É fácil de calcular, as probabilidades sempre são positivas e somam 1.
- Se todas as opções tem a mesma utilidade, as probabilidades de eleição são idênticas.
- Se uma opção tem maior utilidade que o resto, sua probabilidade será mais alta que a do resto. E quanto maior seja a diferença entre utilidades, maior será sua probabilidade de eleição. Isto recorre à ideia de que se a diferença é muito grande, é mais fácil que o erro produza uma mudança nas escolhas.
Como isto nos ajuda em um estudo Conjoint?
A fórmula anterior predisse qual opção escolherá um individuo se conhecemos as utilidades das opções. Um estudo Conjoint trata de resolver o caso contrário: os indivíduos nos dizem quais opções preferem e nós calculamos as utilidades das opções.
Esta fórmula nos da a chave para a análise, como veremos em posteriores posts. Devemos calcular as utilidades que predizem melhor as escolhas que tínhamos observado.
No próximo post abordaremos, por fim, como finalizar um estudo Conjoint. Quais fases compreendem e quais opções temos para cada uma.
Esperamos por você.