Numa época onde praticamente tudo é questionado, a ciência permanece como uma das únicas fontes seguras. Nos chama a atenção quando lemos "Estudos científicos demonstram que..." e as empresas e organizações entenderam essa percepção perfeitamente, por isso utilizam o território científico para demonstrar os benefícios de seus produtos e propostas.
A estatística é um elemento fundamental da ciência, provavelmente a ferramenta que explica o tremendo "boom" que estamos observando a respeito do conhecimento e da tecnologia nos últimos 100 anos.
Porém, a estatística é uma faca de dois gumes, pois pode ser facilmente manipulada quando o público para quem nos dirigimos não conhece bem a linguagem e a base que sustenta o estudo. Como é possível que publiquem estudos onde demonstram que o sal é prejudicial à saúde e, ao mesmo tempo, outros estudos demonstram que o sal é bom? Como as proteínas podem ser boas e más ao mesmo tempo? E a gordura prejudicial e benéfica?
Como fazer com que milhões de pessoas acreditem que o chocolate emagrece
Esse extraordinário post publicado por John Bohannon nos explica como é possível usar a estatística para fazer com que a população acredite em qualquer coisa.
John em parceria com o jornalista Peter Onneken decidiram mostrar ao mundo como funcionam os falsos estudos científicos.
Eles realizaram um estudo com uma amostra reduzida de indivíduos, divididos em grupos:
- Grupo 1 - Indivíduos que realizaram uma dieta com baixo consumo de carboidratos durante 21 dias consecutivos.
- Grupo 2 - Indivíduos que seguiram a mesma dieta do grupo 1, porém consumiram 1 barrinha e meia de chocolate diariamente.
- Grupo 3 - Grupo de controle, pessoas que seguiram com sua dieta habitual.
Depois de estudar os dados a partir de diferentes pontos de vista, John e Peter descobriram que os grupos 1 e 2, perderam cerca de 700 gramas, enquanto 3 grupo não abaixou de peso. O indivíduos do grupo 2 tinham perdido peso 10% mais rápido do que o grupo 1, uma diferença estatisticamente significativa. Além disso, os níveis de colesterol eram melhores junto com algum outro indicador saudável.
BINGO! Já tinham o que eles buscavam: um dado estatisticamente válido que indicava o benefício de comer chocolate na perda de peso. Sem dúvida você deverá estar se perguntando: o que tem de mal esse estudo? Não é assim que funciona a ciência?
A armadilha está num segredinho sobre o uso da estatística num estudo científico: se você mede um grande número dentro de pequeno grupo de indivíduos, você tem quase garantido que poderá encontrar algo "estatisticamente significativo". John mediu seu estudo com 18 parâmetros diferentes (peso, colesterol, nível de sódio) num grupo de... 15 pessoas! O estudo foi projetado para gerar "falsos positivos".
O autor faz uma metáfora que explica muito bem a concepção desse estudo: é como comprar bilhetes de loteria. Cada bilhete tem pouca chance de ser premiado, onde é muito difícil encontrar uma diferença significativa, porém ao considerar apenas 18 parâmetros, suas chances de ser premiado crescem, certo? John não sabia se iria encontrar algo benefício no consumo do chocolate em relação à perda de peso ou pressão arterial, mas tinha certeza que poderia encontrar "algo significativo".
Iremos abordar este tema em posts futuros, porém vamos pensar na expressão "estatisticamente significativo". Está relacionada com algo conhecido como o valor p (p value). Quando obtemos um resultado, sempre relatamos o p value, que é a probabilidade do resultado ser obtido através do acaso. Geralmente considera-se que o resultado é significativo e, por consequência, não será devido ao acaso. Será uma causa substancial se o p value for inferior a 5%.
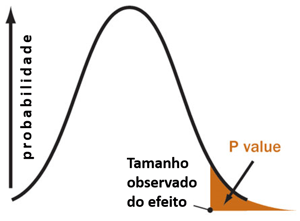 Quando temos um p value abaixo de 5%, obtemos um efeito automático em nossa audiência: a credibilidade do método científico. Quando realizamos um estudo no modelo do John (pouca amostra e muitos parâmetros), a probabilidade dos resultados entre os grupos apresentar diferenças do p value abaixo de 5% aumentam de acordo com a fórmula:
Quando temos um p value abaixo de 5%, obtemos um efeito automático em nossa audiência: a credibilidade do método científico. Quando realizamos um estudo no modelo do John (pouca amostra e muitos parâmetros), a probabilidade dos resultados entre os grupos apresentar diferenças do p value abaixo de 5% aumentam de acordo com a fórmula:
P(winning) = 1 - (1 - p)n
Com n=18, a probabilidade de sucesso é de 60%. Este fenômeno é conhecido como p-hacking. Inúmeros científicos honestos realizam o p-hacking de forma inconsciente. Em algumas ocasiões, quando precisam provar uma hipótese, obtêm alguns resultados negativos e repetem o experimento até que "funcione". É o mesmo problema quando as pessoas compram bilhetes de loteria, até que uma hora, são sorteados.
Como conseguir tanta mídia através de um estudo pouco rigoroso?
A resposta é: "Pouco rigor científico graças à inúmeras publicações combinadas com a mídia sensacionalista". Esta foi a conclusão de John e Peter, onde várias revistas e veículos de comunicação entraram em contato com eles para publicarem sua "descoberta" sem fazer um peer-review (revisão de outro científico). Diversos meios de comunicação publicaram o artigo, por exemplo: Bild ("Os que comem chocolate continuam magros" e outros veículos seguiram o mesmo caminho, como: Daily Star, Irish Examiner, Cosmopolitan’s da Alemanha, Times of India, Huffington Post, canal de TV do Texas e um show de TV australiano.
Um fenômeno curioso observado por John é a forma em que o estudo foi apresentados em diversos meios de comunicação: grande parte acompanhado de imagens "pornográficas" de pessoas comendo chocolate de forma lasciva. Acreditamos que ninguém estava interessado na confiabilidade no resultado, né?
Pouquíssimos veículos contataram a John para conhecer os detalhes do estudo Os poucos que entraram em contato não fizeram a pergunta chave: "Quantas pessoas participaram do estudo?" Se as pessoas soubessem que se tratava de 15 pessoas, sem dúvida o impacto dessa notícia teria sido MUITO diferente.
John e Peter demonstraram, de uma maneira simples, como enganar a opinião pública de forma muito interessante. Agora você já sabe como é feito as notícias e publicações que divulgam "Comer peixes nos deixa mais pacíficos" ou "Ler os rótulos dos alimentos te deixam magro".
Por isso, nós da Netquest, te recomendamos a olhar sempre a ficha técnica do estudo (número de pessoas, reputação, autor da publicação, quem publicou o artigo) e, o mais importante é analisar as hipóteses que suportam os resultados observados. Lembre-se que correlação não é casualidade e muitos estudos estatisticamente bem planejados também confundem ambos os fenômenos.