Continuing with our series of posts on sampling, today we'll review the first random sampling method: simple random sampling. This is one of the most popular sampling methods, and it serves as a reference for many others, even though, as we’ve said before, in practice it can be difficult to implement.
DEFINITION
Simple random sampling (SRS) is a sampling method in which all of the elements in the population—and, consequently, all of the units in the sampling frame—have the same probability of being selected for the sample. It would be along the lines of having a fair raffle among every individual in the population: we give everyone raffle tickets with unique sequential numbers, put them all in a basket and draw numbers from the basket at random. The individuals whose numbers are selected become our sample. Obviously, in practice, these methods can be automated using computers.
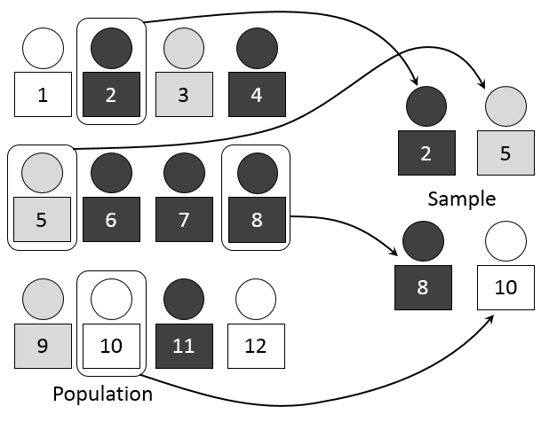
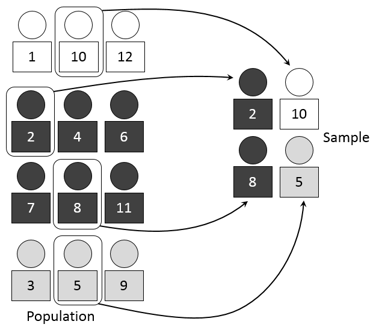
Depending on whether or not the individuals in the population can be selected for the sample more than once, we distinguish between SRS with replacement and SRS without replacement. If we sample with replacement, the fact that an individual was randomly selected for our sample does not prevent that same individual from being chosen again in the next selection. This would be the equivalent of putting the raffle ticket back in the basket after every draw. If, on the other hand, we choose to sample without replacement, an individual selected for the sample is not eligible for the next drawing in the raffle.
To replace, or not to replace? That is the question. It’s a simple math problem. In his book Statistical Sampling (2005), César Pérez López presents a clear comparison between the two methods. In terms of both estimation precision and minimum sample size required to obtain a given level of precision, we can firmly conclude that simple random sampling without replacement is more efficient.
To understand this result, let’s start with the following expression for sample size in an SRS without replacement. The formula below shows the relationship between the sample sizes required to achieve a given level of precision in a finite versus an infinite population:
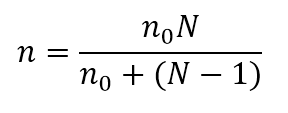
where n0 is the sample size required with an infinite population and N is the size of the finite population. It can be shown that the sample size required when sampling with replacement (nr) is equal to the sample size required when sampling without replacement from an infinite population. (nr=n0). In that case, we can state that
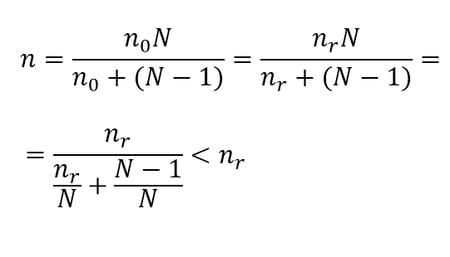
Therefore, the sample size required when we sample without replacement is smaller than the sample size required when we sample with replacement. This makes sense intuitively: if we sample with replacement and the same individual is selected more than once, the effect is similar to reducing the sample size, since the presence of the repeatedly selected individual(s) makes our sample less diverse. Finally, the two sampling methods coincide if the population is infinite, since in that case the odds of selecting an individual more than once in the same sample would be infinitely small.
BENEFITS OF SIMPLE RANDOM SAMPLING
The development of computer science has enabled us to quickly design simple random samples that are extremely reliable. Random numbers generated by software—or, strictly speaking, pseudo-random numbers—are increasingly reliable.
So, by using SRS, we can be sure that we are drawing representative samples, so the only error that could affect our results is chance. Most importantly, we can accurately calculate the likelihood of this error (or at least delimit it). Check out our next post for more information.
DRAWBACK TO SIMPLE RANDOM SAMPLING
The only drawback to SRS is the difficulty of putting it into practice in real-life research. Remember: since it is a probability method, we need a sampling frame that includes all individuals, and all of them need to be selectable for our sample. This is a tough requirement for most real-life market and opinion studies to meet, so researchers for such studies are often forced to use other methods.
In our next post, we’ll take a look at another very popular random sampling method: stratified sampling. See you then!
TABLE OF CONTENTS: Series on sampling
- Sampling: What it is and why it works
- Random and non-random sampling
- Random sampling: Simple random sampling
- Random sampling: Stratified sampling
- Random sampling: Systematic sampling
- Random sampling: Cluster sampling
- Non-random sampling: Availability sampling
- Non-random sampling: Quota sampling
- Non-random sampling: Snowball sampling