In a recent post, we learned about sampling and the advantages it offers when we want to study a population. Today, we're going to take a look at the two main sampling methods. Let’s start by defining the concept of a sampling frame.
Sampling Frame
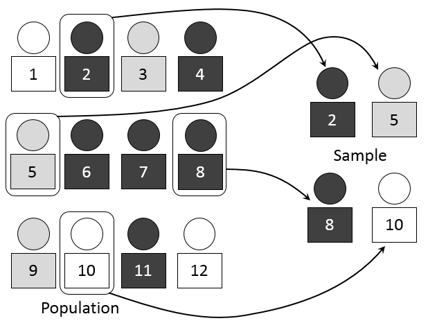
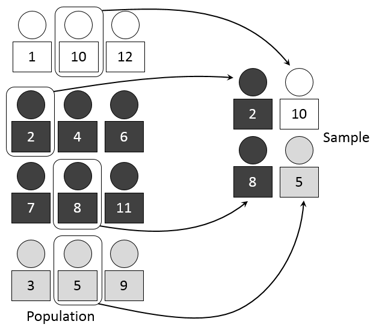
A sampling frame is a list of elements that make up the population that we want to study. The sample is drawn from this list. The elements to be studied could be individuals, but they could also be households, institutions or anything else that might be investigated. The elements within the sampling frame are known as sampling units.
Let’s look at an example. Suppose we want to gauge customers’ satisfaction with a particular business. To create our sampling frame, we could access the business’s computer system and pull up a list of everyone who has purchased a product in the past year. Every individual on that list would be considered a sampling unit. We could then select our sample by choosing a group of these customers.
The proportion of the sampling frame included in the sample is known as the sampling fraction. We saw in an earlier post, that this fraction, along with the sample size, determines the precision of the results that we will obtain by surveying our sample.
Random Sampling
We’re dealing with random sampling whenever the following conditions are met:
-
Every element in our population has a nonzero probability of being selected as part of the sample.
-
We have accurate knowledge of this probability, known as the inclusion probability, for each element in the sampling frame.
If both of these criteria are met, it is possible to obtain unbiased results about the population from studying the sample. To obtain unbiased results, it may sometimes be necessary to use weighting methods; such weighting is possible precisely because we know each individual's probability of being included in the sample. Samples obtained under these conditions are also known as random samples.
The above definition leads us to conclude that we can only create a random sample if we have a sampling frame. A national census, a database of mailing addresses within a city and a list of a business’s customers are all examples of sampling frames that make random sampling possible. In each of the above cases, the population to be studied is different: the residents of a country, the households in a city and a business’s customers, respectively.
Once we have our sampling frame, the random sampling method defines the exact method we will use to select our sample; for example, simple random sampling, systematic sampling, stratified sampling, disproportional stratified sampling, cluster sampling, and so on.
Non-Random Sampling
All that said, it’s not easy to meet the criteria imposed by random sampling:
-
It is relatively unusual to have a sampling frame available to you when you’re conducting market studies.
-
Ensuring that every individual in a population has a nonzero probability of being selected is just as difficult to accomplish; knowing every sampling unit’s exact inclusion probability is even more difficult. The individuals that cannot be selected as part of a sample are generally referred to as excluded units.
For these reasons—and to minimize costs—researchers often turn to other sampling methods, known as nonrandom sampling. When using these alternative methods, researchers generally select elements for the sample based on hypotheses about the population of interest, known as selection criteria. For example, if we’re selecting our sample by stopping people on the street, attempting to stop an equal number of men and women (to coincide with the presumed gender distribution in the population) would be a criterion of nonrandom sampling.
In these cases, since the selection of units for the sample isn’t random, we shouldn’t talk about error estimates. In other words, a nonrandom sample tells us about a population, but we don’t know how precisely: we can’t determine a margin of error or a confidence level.
These types of sampling methods include availability sampling, sequential sampling, quota sampling, discretionary sampling and snowball sampling.
Sampling Errors
As we said above, it is impossible to know the margin of error we’ll have in a study (results from a survey, for example) when we use nonrandom sampling. This includes surveys conducted by selecting passersby on the street and interviewing them face-to-face, by making telephone calls at random or obtained through online panels. None of these cases fulfills the criteria for random sampling: a sampling frame with units for which we can calculate the probability of being selected for our sample. When we conduct live surveys on the street, we don’t have access to a list of the individuals who make up the population.
When we conduct telephone interviews, although we have a list of telephone numbers, not everyone has a landline or a listed number. When we obtain responses from an online panel, individuals who do not have Internet access cannot be selected, and so their inclusion probability is zero.
Nevertheless, we regularly come across studies conducted using these methods that state a margin of error and a confidence level. Formally speaking, this is an incorrect practice, but researchers tend to use it in order to give some indication of the influence that the sample size has on the precision of the results. It would be more accurate to say, “if this were a random sample, it would have margin of error equal to X.”
There is a wide range of opinions over the usefulness of stating a margin of error under these circumstances, as expressed in a debate described in the next post.
In the next few posts, we’ll take a look at each of the sampling methods in turn: how they work, what they are used for and what kind of results they provide.
TABLE OF CONTENTS: Series on sampling