Now that we have taken a look at stratified sampling, we’d like to continue our series of posts on sampling techniques by examining systematic sampling.
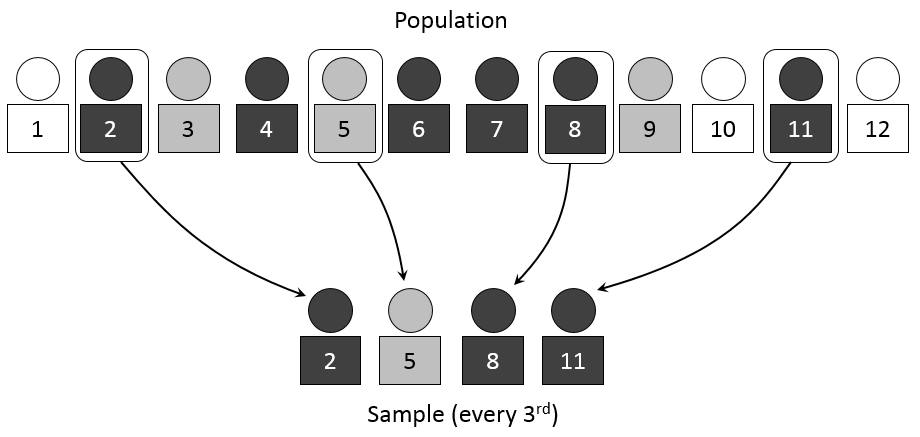
Systematic sampling used to be very popular, before computer science solved one of researchers’ biggest headaches: randomly selecting individuals from within a sample. Now that computers can generate random numbers, this problem has vanished.
It is still used, however, to select individuals over a period of time. For example, if we want to study satisfaction with a service at a store, we can systematically survey one out of ever n customers who visit. In these cases, in which the variance between individuals could be different at different moments, systematic sampling can be even more precise than pure simple random sampling.
How Does Systematic Sampling Work?
Systematic sampling is one method in the broader category of random sampling (for this reason, it requires precise control of the sampling frame of selectable individuals and of the probability that they will be selected). It involves choosing a first individual at random from the population, then selecting every following nth individual within the sampling frame to make up the sample.
Systematic sampling is a very simple process that requires choosing only one individual at random. The rest of the process is fast and easy. As with simple random sampling, the results that we obtain are representative of the population, provided that there is no factor intrinsic to the individuals selected that regularly repeats certain characteristics of the population every certain number of individuals—which is very rarely the case.
The Process
The process for conducting systematic sampling is as follows:
1. We prepare an ordered list of N individuals in the population; this will be our sampling frame.
2. We divide the sampling frame into n fragments, where n is our desired sample size. The size of these fragments will be
K=N/n
where K is called the interval or lift coefficient.
3. The initial number: we randomly obtain a whole number A, which is less than or equal to the interval. The number corresponds to the first subject who we select for the sample within the first fragment into which we have divided the population.
4. Selection of the remaining n-1 individuals: We select the subsequent individuals based on where they fall, in simple arithmetic succession, after the randomly selected individual, selecting individuals who occupy the same position as the initial subject in the rest of the fragment into which we have divided the sample. This is the equivalent of saying that we will select the individuals
A, A + K, A + 2K, A + 3K, ...., A + (n-1)K
Example
Let’s say that our sampling frame includes 5,000 individuals and we want a 100-individual sample. First, we divide the sampling frame into 100 fragments of 50 individuals. Then, we randomly select one number between 1 and 50 in order to randomly select the first individual for the first fragment. Let's say we select 24. The sample is defined by this individual; we select the remaining individuals from the list at intervals of 50 units:
24, 74, 124, 174, ..., 4.974
Properties Of Systematic Sampling
The main advantages are:
- It offers good representative properties that are similar to, or even better than, those obtained through simple random sampling, but in a faster and simpler way, since there is no need to generate a random number for each individual in the sample.
- Unlike random sampling, systematic sampling guarantees perfectly even selection from the population. This can be useful if we distinguish groups within the population, thus avoiding the need to use strata. If there is different variance between the individuals in the fragments, systematic sampling could be better than random sampling. We’ll take a look at this a bit later.
The only disadvantage is the one we mentioned earlier: the off chance that the order in which the candidates are listed in the sample somehow repeats a patter than unwittingly coincides with the interval chosen to create the systematic sample. If this is the case, we may end up with a biased sample.
The Effectiveness Of Systematic Sampling
They originally thought up systematic sampling as a way of improving upon simple random sampling, but just how much of an improvement it offers depends on the properties of the population being studied.
There is something that you must bear in mind if you want to understand this sampling method: if we determine the interval or lift coefficient based on the sample size we need, the only random element within the sampling process is the initial unit that we selected from the first block of individuals. The rest is already determined. This means that we can only obtain k unique possible samples and that sampling is merely a matter of choosing one of the samples available to us.
It is possible to demonstrate that the more the variance within the k possible samples exceeds population variance, the more precision we will achieve using systematic sampling, rather than simple random sampling. Systematic sampling is more precise than simple random sampling whenever the variability within the possible samples is greater than the variability among the population units. Systematic sampling and simple random sampling have the same precision when their respective variabilities coincide, which occurs when the order of the elements within the population are totally random.
TABLE OF CONTENTS: Series on sampling